Communications Toolbox 学习记录 二 :OFDM 入门
少说废话,现在开始看看下一个案例吧!
这篇只写一个案例,因为这个案例还是比较复杂的,分成了多个步骤
案例:matlab 仿真OFDM系统
正交频分复用 (OFDM) 是现代无线通信系统(如 5G 和 LTE 蜂窝以及 WiFi)使用的多载波数字调制技术。
与单载波 QAM 等其他技术相比,OFDM 的优势包括支持更高的数据速率和更简单的接收器设计。
具体而言,使用带有循环前缀 (CP) 的 OFDM 可以实现基于快速傅里叶变换 (FFT) 的均衡和同步,与用于在单载波 QAM 中接收可比数据速率的技术相比,这简化了接收。
1、OFDM 介绍
正交频分复用 (OFDM) 通过将调制的高带宽信号载波划分到许多调制的窄带子载波上来实现高数据速率传输。对于 OFDM 传输,窄带子载波的使用降低了对频率选择性衰落的敏感度。许多最新的无线和电信标准都使用多载波 OFDM 调制格式。
在单载波系统中支持高数据速率需要宽带载波,有较短的符号持续时间。宽带载波通过频率选择性多径信道过滤宽带宽载波会严重降低信号质量,因为信道脉冲响应在时间上跨越多个符号并使信号容易受到符号间干扰 (ISI) 的影响。
为了避免在传输许多并行低带宽信号时出现 ISI,各个子载波必须相互正交。通过传输许多正交低带宽子载波来避免 ISI 激发了 OFDM。OFDM 调制器将高速率串行符号流转换为许多并行低速率流。每个正交低速率流遇到一个具有最小 ISI 的相对平坦的信道,并且可以很容易地均衡。
举个例子:
一个信号,其脉冲持续时间为$T_{sym}=0.25 sec$,那么符号速率为$R_{sym}=1/T_{sym}=8Hz$,
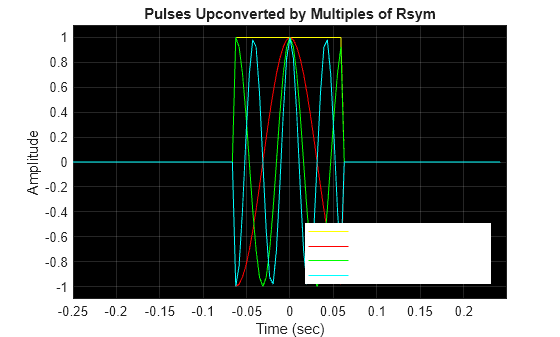
将这个脉冲乘以数倍于$R_{sym}$ 如 频率为$R_{sym}、2R_{sym}、3R_{sym}$的余弦波,得到下图:
时域图:
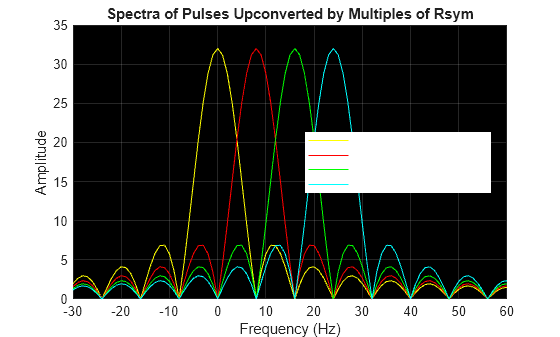
频域图:
可以发现,每个子载波的频谱峰值出现在所有其他脉冲的过零处。
OFDM 调制器将所有这些子载波加在一起以形成其输出信号。子载波数据可以用不同的调制方式。
这里,子载波使用 QAM 方法进行基带调制。
数学上,OFDM调制符号采样输出为
其中
- $a_{m, n}$是第$n$个(时域)OFDM调制符号的第$m$个子载波的 符号
- $R_{\mathrm{sym}}$是每个QAM符号流的符号速率
- $T_{\mathrm{sym}}=1/R_{\mathrm{sym}}$
- $N$是子载波的数量 或者说是QAM符号流的数量
公式也可以简写为
这数学上恰好与$a_{m, n}$的离散傅里叶反变换不谋而合。
2、没有循环前缀的OFDM 仿真
首先,OFDM符号我们采用 OFDM 子载波数据用QAM调制的方案,将这些数据作为子载波前面的系数,然后利用快速傅里叶反变换(IFFT),将并行传输的数据 转换为一个个相互正交的子载波的叠加。因为每一个子载波传输的数据非常少(一个OFDM符号周期才传输一个QAM符号),所以每个子载波都是窄带的,所以大概里经历平坦衰落,接收端的均衡器均衡器每个子载波仅需要一个抽头。
这是一个16QAM+OFDM的程序仿真
2.1、信源端
bps = 4; % Bits per symbol
M = 2^bps; % 16QAM
nFFT = 128; % Number of FFT bins
txsymbols = randi([0 M-1],nFFT,1);
txgrid = qammod(txsymbols,M,UnitAveragePower=true);
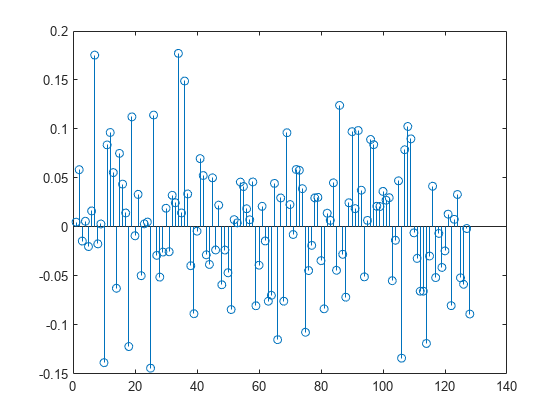
txout = ifft(txgrid,nFFT);
stem(1:nFFT,real(txout))2.2、信道
rxin = awgn(txout,40);
rxgrid = fft(rxin,nFFT);
rxsymbols = qamdemod(rxgrid,M,UnitAveragePower=true); if isequal(txsymbols,rxsymbols)
disp( "恢复的符号与传输的符号匹配。" )
else
disp( "恢复的符号与传输的符号不匹配。" )
endIFFT 的所有 bin(应该是指输入系数) 都填充有用数据。在实际系统中,边缘端子载波通常留空以用作保护带,并且一些子载波 可用于发送特定的导频信号。保护带和导频信号的组合有助于同步和均衡。
3、均衡、卷积、以及循环前缀
3.1、频域均衡
这个例子介绍了频域均衡,并展示了如何将循环卷积“转换”(其实不叫转换,得到前len(u)个想要的结果)为线性卷积
当考虑线性信道模型时,接收信号是发射信号与信道脉冲响应的卷积。
也即:
只要知道了频域相应$H(f)$,就还可以得到信号,即
其实这个式子就是频域均衡
3.2、卷积
但是FFT处理产生的其实是信号$u$和$h$的循环卷积(这是为啥?),为了将这种循环卷积转换为线性卷积,$u$,$h$填充零的个数至少到 length(u)+length(h)-1 (填零策略)
如果得到的必是循环卷积,那么,子载波数量N应该是len(u)+len(h)-1,
eg:输入8个数据,信道冲击为3径,那么N至少为8+3-1=10
也就是填2个0
看一个循环卷积和线性卷积的区别例子
u1 = 1:8;
h = [0.4 1 0.4];
figure
subplot(2,1,1)
stem(u1);
axis([0 10 0 10])
title("Input signal")
subplot(2,1,2)
stem(h);
axis([0 10 0 2])
title("Channel impulse response")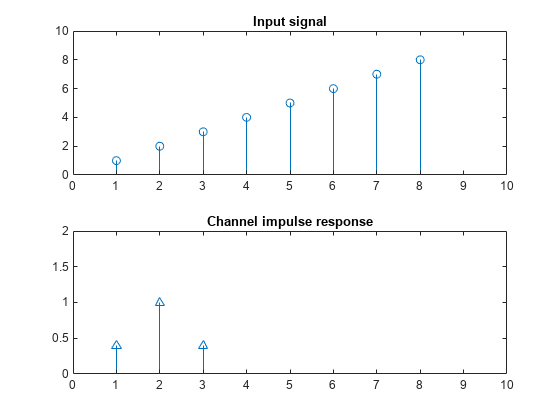
循环前缀能够把信道消弭未知信道时延的影响(循环长度大于最大信道时延长度即可)
3.3、循环前缀
对于 OFDM 处理,循环卷积的必要填充是通过添加 CP 而不是对信号进行零填充来提供的。添加重复符号结束样本的 CP 可启用:
- 通过IFFT&FFT计算的卷积转换为循环卷积
- 用于信道估计、均衡和同步的简单频域处理
- 用于前向纠错方案的重复样本
L = length(h); % Length of channel
N = length(u1); % Length of input signal
ucp = u1(N-L+1:N); % Use last samples of input signal as the CP
u2 = [ucp u1]; % Prepend the CP to the input signal
yl2 = conv(u2,h); % Convolution of input+CP and channel
yl2 = yl2(L+1:end); % Remove CP to compare signals
figure;
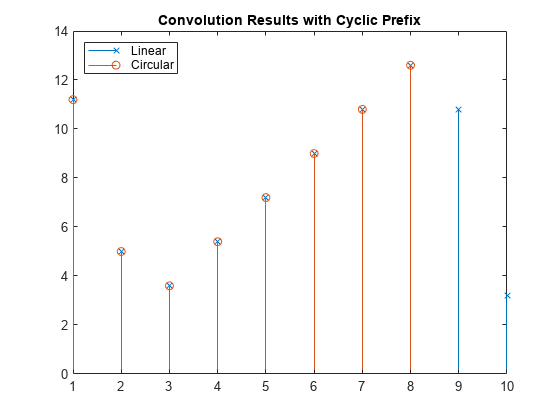
stem(yc1,"x")
hold on;
stem(yl2,"o")
title("Convolution Results with Cyclic Prefix")
legend ("Linear","Circular","Location","northwest")对比循环卷积与线性卷积的误差使得否达到要求
if max(yc1 - yl2(1:N)) < 1e-8
disp("Linear and circular convolution sequences match.")
else
disp("Received symbols do not match transmitted symbols.")
end4、加CP的OFDM仿真
在这个案例中,将构建一个带有循环前缀的16QAM & OFDM 仿真
为了能有效的均衡,循环前缀的长度必须大于信道长度(上一节说了,只有填零或者前缀的个数大于len(u)+len(h)-1 才有可能将循环卷积“转换”为线性卷积)
4.1、基本参数
定义 QAM 和 OFDM 处理的变量。生成符号、QAM 调制、OFDM 调制,然后将 CP 添加到信号中。多个OFDM符号可以同时处理然后串行化。
bps = 4; % Number of bits per symbol 相当于之前的k = log2(M)
M = 2^bps; % Modulation order
nFFT = 128; % Number of FFT bins
nCP = 8; % CP length4.2 发射端
txsymbols = randi([0 M-1],nFFT,1);
txgrid = qammod(txsymbols,M,UnitAveragePower=true);
txout = ifft(txgrid,nFFT);
% To process multiple symbols, vectorize the txout matrix
% 这一步不太明白,我测试了一下,好像有没有这一句没区别啊!
txout = txout(:);
% 取cp、加cp
txcp = txout(nFFT-nCP+1:nFFT);
txout = [txcp; txout];4.3、噪声部分 (噪声、频选、延迟)
hchan = [0.4 1 0.4].'; % 信道冲激响应
rxin = awgn(txout,40); % Add noise
rxin = conv(rxin,hchan); % Add frequency dependency
channelDelay = dsp.Delay(1); % Could use fractional delay 我发现效果就是第一个数据是零后面的数据是原数据往后移动一位
rxin = channelDelay(rxin); % Add delay4.4、接收端
添加一个小于 CP 长度的随机偏移量。零模型的偏移设置可在发射和接收信号之间实现完美同步?。任何小于 CP 长度的时序偏移都可以通过额外的线性相位进行均衡补偿。
[这个偏移量offset 到底有什么用?为什么设成随机的,难道是信道参数吗??]
答:
- 1、可能是模拟了一个信道产生的频偏,是信道参数。
- 2、可能是同步时产生的误差(没有找到正确的OFDM信号开始的位置)
(以下结论参考自北京大学赵玉萍OFDM系统的频偏与时篇PPT) - 载波频率偏移对于低频信号的作用相当于在OFDM时域采样序列上增添了一个等效指数因子
- 该因子是随着时间连续变化的,即 n = 0 ~ N
- 频偏对系统的影响可写为归一化频偏的函数$\epsilon=df/\Delta f$($\Delta f$是子载波间隔、$df$是频偏)
offset = randi(nCP) - 1; % random offset less than length of CP
% Remove CP and synchronize the received signal
% 下面这一步1、去掉了CP头,2、假设完美同步(时延消除)3、往前多了 offset
rxsync = rxin(nCP+1+channelDelay.Length-offset:end);
rxgrid = fft(rxsync(1:nFFT),nFFT);至于为什么取rxsync = rxin(nCP+1+channelDelay.Length-offset:end); 就能表示频偏还是不太明白。
可能的推导思路:
设发射端经过IFFT变换之后传输信号为:
若接收信号存在频率偏移, 此时信号应表示为
$\boldsymbol{w}(n)$ 为高斯噪声的取样值
% 是否使用均衡?
useEqualizer = true;
if useEqualizer
hfchan = fft(hchan,nFFT);
% 毫无疑问,hfchan是信道的频域相应,
% Linear phase term related to timing offset
offsetf = exp(-1i * 2*pi*offset * (0:nFFT-1).'/nFFT);
%这一步好像是给信号应该是将原来的频偏给消除了
rxgrideq = rxgrid ./ (hfchan .* offsetf);
else % Without equalization errors occur
rxgrideq = rxgrid;
end
rxsymbols = qamdemod(rxgrideq,M,UnitAveragePower=true);
if max(txsymbols - rxsymbols) < 1e-8
disp("Receiver output matches transmitter input.");
else
disp("Received symbols do not match transmitted symbols.")
end
5、the final - matlab OFDM 仿真
5.1、 基本配置
k = 4; % Number of bits per symbol
M = 2^k; % Modulation order
nFFT = 128; % Number of FFT bins
cplen = 8; % CP length5.2、 发射端
txsymbols = randi([0 M-1],nFFT,1);
txgrid = qammod(txsymbols,M,UnitAveragePower=true);
txout = ifft(txgrid,nFFT);
txout = txout(:); % Vectorize matrix if processing multiple symbols
txcp = txout(nFFT-cplen+1:nFFT);
txout = [txcp; txout];- 一个OFDM符号的时间长度$T_{symbol}$是子载波间隔$\Delta f$的倒数(因为OFDM符号是各个子载波信号在时域上的叠加,所以一个符号时间就是一个子载波的符号周期,而一个子载波的符号时间等于器在载波间隔的倒数)
- 一个OFDM符号我们用N(nFFT)个采样点表示 这里是128点
- 所以采样点之间的时间间隔为 $T_{symbol}/N$ , 采样频率为 $N \Delta f $,所以这里为什么除以2呢????奇怪。
scs = 20e3; % Subcarrier spacing in Hz 子载波间隔?
Fs = scs * nFFT/2; % Sampling rate (1.28e6 Hz) 采样频率
Ts = 1 / Fs; % Sample duration in seconds Tend = Ts * (length(txout)-1);
subplot(211)
hold off
plot(0:Ts:Tend,real(txout),"*")
title("Real component of transmitter output")
subplot(212)
hold off
plot(0:Ts:Tend,imag(txout),"*")
title("Imaginary component of transmitter output")5.2.1、 过采样
Define an FFT length longer than nFFT to cause oversampling in time domain. To aid comparison later, insert zeros into the middle of txgrid to maintain correspondence between bin centers for the original and upsampled signals. A control here allows you to adjust the integer oversampling rate used by the OFDM modulator output and demodulator input.
定义一个长度大于nFFT的 FFT,这样可以在时域上过采样。为了便于比较,在 txgrid 的中间插入零以保持原始信号和上采样信号的 bin 中心之间的对应关系(为什么?)。upFactor 是过采样倍数可以自行调整
% 我更改了以下填零的顺序,发现并没有太大的变化,都能拟合
是那么叫保持原始信号和上采样 信号 系数中心之间的对应关系?有什么样的对应关系需要保持呢?
答:在IFFT变换矩阵中,每行的前一半都是正频率而后一半都是负频率。因此,若要使用过采样,就应该将0添加到输入数据的中间而非末尾 —— 这样就能够确保添加的0数据值被映射到正和负频率一半的子载波上,而非0数据则被映射到0Hz附近的子载波上 参考资料 ,
呃 还是没懂 ,他妈的
upFactor = 3;
nFFTUp = upFactor * nFFT;
fftgrid = [txgrid(1:nFFT/2); ...
zeros((upFactor-1)*nFFT,1); ...
txgrid((nFFT/2+1):nFFT)];
% Each column of fftgrid is one OFDM symbol
txout = upFactor * ifft(fftgrid,nFFTUp);
% Vectorize the matrix to process multiple OFDM symbols
txout = txout(:);
cplenUp = cplen * upFactor;
txcp = txout(nFFTUp-cplenUp+1:nFFTUp);
txout = [txcp; txout];
Ts = 1 / (upFactor*Fs);
Tend = Ts * (length(txout)-1);
subplot(211)
hold on
plot(0:Ts:Tend,real(txout))
legend ("Original","Upsampled","Location","southeast")
subplot(212)
hold on
plot(0:Ts:Tend,imag(txout))
legend ("Original","Upsampled","Location","southeast")5.3、信道
hchan = [0.4 1 0.4].'; % 信道冲击
rxin = awgn(txout,40); % Add noise
rxin = conv(rxin,hchan); % Add frequency dependency
channelDelay = dsp.Delay(1); % Could use fractional delay 时延
rxin = channelDelay(rxin); % Add delay添加一个小于 CP 长度的随机偏移量。零模型的偏移设置可在发射和接收信号之间实现完美同步。任何小于 CP 长度的时序偏移都可以通过额外的线性相位进行均衡补偿。为了直接比较不同速率的信号,在 FFT 处理之前,通过上采样因子对同步信号进行归一化。
offset = (randi(cplenUp) - 1); % random offset less than length of CP
% Remove CP and synchronize the received signal
rxsync = rxin(cplenUp+1+channelDelay.Length-offset:end);
rxgrid = fft(rxsync(1:nFFTUp),nFFTUp)/upFactor;5.4 接收端均衡
useEqualizer = true;
if useEqualizer
%注意,接收端iFFT采用的是 nFFT×过采样倍数 的点数!!!!!!!!
hfchan = fft(hchan,nFFTUp);
% Linear phase term related to timing offset
offsetf = exp(-1i * 2*pi*offset * (0:nFFTUp-1).'/nFFTUp);
rxgrideq = rxgrid ./ (hfchan .* offsetf);
else % Without equalization errors occur
rxgrideq = rxgrid;
end
rxgridNoZeroPad = [rxgrideq(1:nFFT/2); ...
rxgrideq((1+(upFactor-0.5)*nFFT):end)];% 取前nFFT/2个,取后nFFT/2个
rxsymbols = qamdemod(rxgridNoZeroPad,M,UnitAveragePower=true);
if max(txsymbols - rxsymbols) < 1e-8
disp("Oversampled receiver output matches transmitter input.");
else
disp("Received symbols do not match transmitted symbols.")
end这一小节先到这里啦~ 还有n多问题没有解决 555,主要集中在:
1、设置的偏移上(offset),rxsync = rxin(cplenUp+1+channelDelay.Length-offset:end); 这里的意义
2、过采样的时候,在iFFT前 为什么中间填零,而不是两边?
3、3径信道的影响没看到呀,哦哦,可能是OFDM以为天然抵抗多径,所以没啥影响。
后续知道答案时会及时解决