语音信号处理(三)自适应滤波方法
自适应滤波 是一种理论体系,应用于内容都非常广泛
滤波器
作用:改变信号的频谱
- 模拟滤波器:由R、L、C构成的模拟电路,例如A/D前的抗混叠滤波器(anti-alias filter)
- 数字滤波器:由数字加法器、乘法器、延时器构成,基于数字信号运算实现。(数字通信系统中,不做特殊说明时 一般都指数字滤波器)
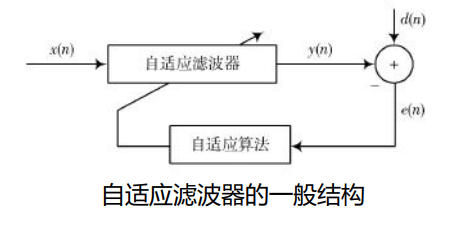
自适应滤波器:一种能够根据输入信号自动调整自身参数的数字滤波器。
非自适应滤波器:具有静态滤波器系数的数字滤波器,这些静态系数构成了滤波器的传递函数。- 自适应滤波器的应用场景:无法得知输入信号和噪声统计特性的情况(也即非平稳信号)。滤波器自身能够在工作过程中学习或估计信号的统计特性,并以此为依据调整自身参数,以达到某种准则/代价函数下的最优滤波效果。此外还能跟踪信号变化。
- 自适应滤波器的应用场景:无法得知输入信号和噪声统计特性的情况(也即非平稳信号)。滤波器自身能够在工作过程中学习或估计信号的统计特性,并以此为依据调整自身参数,以达到某种准则/代价函数下的最优滤波效果。此外还能跟踪信号变化。
一、LMS(最小均方误差)算法
这是一个最基本的自适应滤波的算法,应用多,原理也比较简单。
1.1、 从N阶线性系统出发
设一个信号经过噪声因素被接受为$x(n)$
设接收信号$x(n)$通过了一个N阶滤波器,参数为{$w_i(n)$},则滤波器输出为:
后面两种是卷积结果(的一个时刻,n时刻)的向量表示(可以动手写一些是不是这样)
其中
注意到,由于滤波器系数$w(n)$是随着时间n变化的,也即随着输入变化不断“学习”的,所以每个时刻的滤波器系数应当不同,所以写为时间的函数。
期望输出为$d(n)$,定义误差信号:
我们定义的误差采用的滤波器系数是当前时刻的,这种误差在传统的自适应滤波器算法当中也叫后验误差,这里后验的意思就是算当前误差的时候已经用到了当前时刻的滤波器系数向量了。
现在已经定义了误差,那么下一步就是寻找某种优化准则,以及基于这个准则,定义一种目标函数来最小化这个目标函数即可。
自适应滤波当中最常用的准则就是MMSE(最小均方误差准则),在这种准则下面就可以很自然的定义目标函数:将目标函数写成均方误差的形式,目标函数如下:
1.2、维纳滤波
为了最小化目标函数, 需要计算$J(\mathbf{w})$对$\mathbf{w}$的导数,并令导数为零,结果如下:
其中 $\mathbf{R}=E\left\{\mathbf{x}(n) \mathbf{x}^{T}(n)\right\} $,$\mathbf{r}=E\{\mathbf{x}(n) d(n)\}$
矩阵$\mathbf{R}$就是输入的 期望自相关矩阵,而$\mathbf{r}$是输入信号与期望信号的 相关向量
那么再MMSE准则下,最优的滤波器学习系数就是
得到的解叫做维纳解,也是在MMSE意义下的最优解,以这种解为系数的滤波器称为Wiener滤波器。
Wiener滤波器是一种在信号处理领域极具理论价值的滤波器,但是,在实际应用过程中却又诸多缺陷。
- 首先:不适用于非平稳过程(因为 相关矩阵 和相关向量 都是期望的形式),语音信号就是非平稳信号
- 再求解过程中需要用到信号的所有历史数据(包括自相关矩阵,以及相关向量),(当信号是非平稳的时)当增加一个数据过后,滤波器就要重新求解系数。(或者在已知所有 输入以及期望信号的情况下,一次性算出 滤波器系数,是一种静态滤波器,不能跟踪变化)
如果对于上述过程还是不太理解,也可以翻阅知乎的这篇博客
1.3、自适应滤波器( 迭代算法,LMS算法)
由于涉及数学期望,在实际应用中,绝大多数情况下我们无法获得信号真实的自相关矩阵以及输入信号与期望输出之间的互相关向量,因此,实际应用中,我们用下式的瞬时梯度的迭代更新方案,代替数学期望方案,PS:梯度隐含着这是一个可导函数,梯度是一个向量(隐含了大小和方向),方向是函数值变化(上升)最快的方向向量,大小是变化的快慢。
求取的瞬时梯度(的负梯度方向)代表了滤波器系数应该调整的方向,也就是误差下降的方向
于是,我们得到了标准时域LMS算法的更新公式:(也即基于采样点更新的标准LMS算法滤波器系数更新公式)
其中,$2\mu $表示调整步长 ,由于是一个可变可调的参数,大部分文献也写z整体直接写为$\mu$。
关于LMS算法步长的取值范围, 这里不给推导的给出:
$\lambda_{max}$为 输入信号$x(n)$的自相关矩阵$\mathbf{R}$的最大特征值;
PS:求特征值可以用matlab eig(函数)
rho_max = max(eig(input_ref'*input_ref)); % 输入信号相关矩阵的最大特征值为了避免求特征值的麻烦,有时也可以用矩阵的迹$t_r(\mathbf{R})=\sum \lambda=\sum^{L}_{k=0} x^2(k)$来替代。 即$0<\mu<t_r(\mathbf{R})$
标准LMS算法的执行流程:
步骤:
1) 滤波器初始化:
2) 对每一个新的输入采样 ,计算输出信号
3) 利用期望输出 ,根据误差公式计算误差信号 ,得到梯度(更新向量)
4) 利用LMS算法的更新公式更新滤波器系数:
5) 返回步骤 2,直至结束,可以得到输出序列和误差序列。
LMS算法的基本思想 ——梯度下降
LMS使用瞬时梯度作为每一步滤波器向量更新的依据,由于瞬时梯度就是目标函数真实梯度的无偏估计,这样这样保证了标准LMS算法的总体更新趋势使目标函数达到最小
LMS算法的优缺点:
优点:简单,易于实现
缺点:收敛速度慢(虽然 瞬时梯度是 真实梯度的无偏估计,但是估计的方差不为零,估计方差存在误差(噪声),这种方差的存在导致了LMS收敛速度比较慢)
代码实现
function [y,e,w]=MyLMS(L,mu,x,d)
% 输入参数
% L 滤波器阶数
% mu 学习步长; 一般玄奇
% x 输入信号; 是指 直接进入滤波器于滤波器系数相卷积的那一路
% d 期望信号:是指 不进入滤波器,而只作为“参考”,产生误差信号的那一路
% output 输出:是指滤波器的直接输出
% w 滤波器系数:
% 注意 输入信号于期望 输入应该保证一样长
N=length(d); % 总输入长度
w = zeros(1,L); % 行向量
e=zeros(1,N);
y=zeros(1:N);
x = [zeros(1,L -1) x']; % 行向量
for n = 1:N % 每一个采样点“前进一步”
m = n + L -1; % n是“起始点”,m则是“结束点”
xpad = x(m-L+1:1:m)';
% 列向量 :看x 的定义中,要把x做翻褶才对 就是x=【xn xn-1 ……xn-L+1】
% 但是 也可以定义“w 是做了翻褶之后的结果” 即 w = 【wL-1,wL-2,……w0】,那么 x就可以不用翻褶了
% 对于后续的影响:由于见每一句备注
y(n) = w*(xpad); % 滤波器输出 y=w*x ,由于得到的是一个数,所以对时序没有影响
e(n) = d(n) - y(n); % 误差信号 e=d-y
w = w + mu.*xpad'.*e(n); % 调整滤波器系数的LMS算法 w=w+mu*x*e , 根据一一对应关系,没有影响,就是注意w是翻褶后的结果
end
end1.4、LMS衍生算法(一): block LMS (BLMS) 分块最小均方算法
- 思想:由于标准的LMS算法 每一个采样点都进行更新,那么有一种思路就是:不必每一个采样点都进行更新,而是累积到一定数量的采样点之后再进行更新,而对于这些block采样点再更新一次滤波器系数。 这样的好处就是每一个block 获取的梯度是 一个block所有采样点梯度的求和,所以得到的梯度仍然是 真实梯度 的无偏估计 ,但是累计的采样点数更多,他的方差会更小。
- 这种 想法与深度学习里面的minibatch的想法一致。
- 关于梯度噪声,梯度噪声的存在并非完全没有好处,梯度噪声可能会帮助我们跳出一些局部最优值,从而向全局最优的方向进行移动。
用更多的采样点,更新一次滤波器系数
$\mathbf{w}(n+1)=\mathbf{w}(n)+2 \mu \mathbf{x}(n) e(n)$
$\mathbf{w}(n+2)=\mathbf{w}(n+1)+2 \mu \mathbf{x}(n+1) e(n+1)$
$\cdots \cdot$
$\mathbf{w}(n+L)=\mathbf{w}(n+L-1)+2 \mu \mathbf{x}(n+L-1) e(n+L-1)$
不难得出时域LMS的分块更新(block recursion)公式
每 L 点更新一次
注意,式中的误差信号是通过同一个滤波器 得到的:
即$n+m$时刻($0<=m<L$)的误差都是由$n$时刻的滤波器系数得到的,而不是标准LMS中的$n+m$时刻(当前时刻)
为了推导方便,我们通常令 L=N 也就是跟新块的长度就等于滤波器阶数。
与标准LMS算法相比,block LMS的更新频率降低了L倍,所以,我们定义一个新的时间索引k 来代替n。$kL=n$
那么上式的跟新方程可以用下式代替:
其中将w(kL)和w(kL+1)分别简写成w(k)和w(k+1)。那么, block LMS的梯度其实是block中每个点的梯度求和如下
block LMS 的核心运算:
- 计算误差时:就是输入向量与滤波器系数的卷积
- 计算block梯度时:实际时输入向量与误差向量的相关
1.5、LMS衍生算法(二):frequency-domain adaptive filtering (FDAF) 频域自适应滤波
上一小节最后,说到BLMS核心运算就是卷积和相关。
但是,时域的卷积或者相关操作的复杂度时比较高的,一般我们更愿意将时域的卷积或者相关运算换算到频域(时域相关对应于频域相乘)来操作从而减少计算量,这也就是频域LMS算法的思想。
回顾 圆周卷积/相关 与 线性卷积/相关 的关系
圆周卷积与线性卷积
一般的,如果两个有限长序列的长度为$N_1$和$N_2$ ,且满足$N_{1} \geqslant N_{2}$ ,则有圆周卷积的后$N_1-N_2+1$ 个点,与线性卷积的结果一致。
第一步计算线性卷积:
目标利用FFT计算线性卷积。 有以下两种方案:
- overlap -save method (重叠保留法)
overlap -add method (重叠相加法)
重叠保留法 以求BLMS求卷积部分为例
为了得到$N$点的(线性卷积后的)输出信号:
以由于$N_1>=N_2$(也就是输入信号长度通常要大于等于滤波器阶数),且$N_2=N$(滤波器阶数为N),那么就要求每次参与运算的输入信号长度$N_1$至少为$2N-1$,为了FFT计算方便我们令输入长度为$N_1=2N$
那么FFT的点数就为$2N$
如何扩展到2N长呢?
- 对于输入信号而言, 除了当前N个采样点之外,还需要向前取N个点采样值
- 对于滤波器来说,在N阶滤波器后面补N个0 即可
然后分别计算二者扩展后的傅里叶变换,频域相乘后反变换 就能得到2N长的圆周卷积
对于想要的N长的线性卷积,就是得到的圆周卷积的后N个点
$\mathbf{y}(k)=[y(k N), y(k N+1), \ldots, y(k N+N-1))]=$ last $N$ samples of $\mathbf{F}^{-1} \mathbf{Y}(k)$
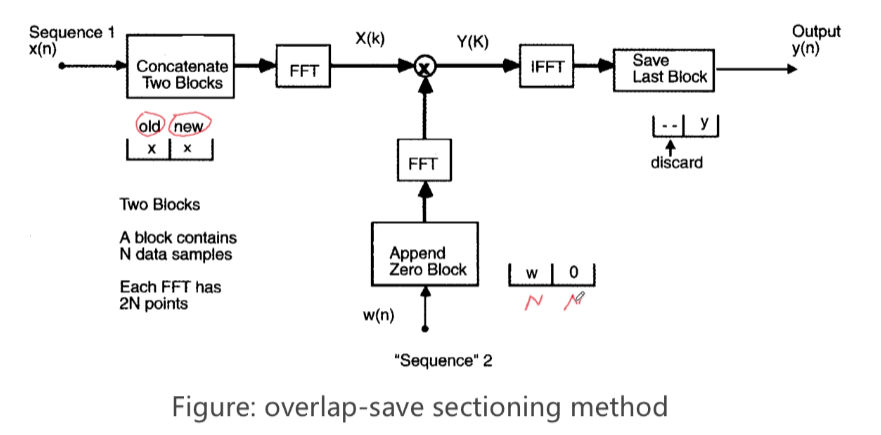
下面就是流程框图:
注意,overlap-save方法不仅适用于频域自适应滤波,对于滤波器系数固定不变的情况依然适用。例如我们常见的语音加混响,其实就是计算纯净语音信号,与固定系数的房间冲激响应之间的线性卷积,可以使用overlap-save方法实现。
圆周相关与线性相关
一般的,如果两个有限长序列的长度为 $N_1$和$N_2$ ,且满足$N_{1} \geqslant N_{2}$,则有圆周相关的前$N_1-N_2+1$ 个点,与线性相关的结果一致。
第二步 计算线性相关
与对卷积的操作非常类似,为了计算输入向量与误差信号之间的线性相关,我们的思路仍然是想办法将它们变换到频域,计算输入信号的共轭谱与误差信号谱的乘积,在进行逆变换到时域。
步骤
- 1、获取$\mathbf{x}(k)$ ,以及其傅里叶变换 这在上一步 已获得,(所以注意这是扩展之后的长为2N的输入信号)即
- 2、扩展误差信号,对于误差信号($\mathbf{e}(k)=[e(k N), \quad e(k N+1), \ldots, e(k N+N-1)]$)也需要将器扩展到2N长度
- 思考:计算卷积的时候,我们将滤波器系数向量后面补N 个零。
并计算扩展误差信号的傅里叶变换:那么,计算相关的时候,我们在误差向量前面补N 个零。(这是为什么?:因为圆周卷积有一个“翻褶”的操作,而圆周相关没有?)
- 思考:计算卷积的时候,我们将滤波器系数向量后面补N 个零。
3、将 上述 二者 频域相乘 (注意时共轭相乘)
4、取逆变换后前N点
对于想要的N长的线性相关,就是得到的圆周卷积的前N个点,也即
第三步 滤波器系数更新
求了上述梯度后,仅需按照时域跟新方程更新即可。至此,BLMS的连个关键问题已经被解决
但是,每次更新都要进行多次的时频转换,最终转换到时域进行更新,为什么不直接在频域范围里进行更新呢?这也就是频域自适应滤波frequency-domain adaptive filtering (FDAF)的思想。
具体而言就是把原来是时域更新方程
改写为:
注意:
- 第一,滤波器系数直接在频域更新,所以需要将梯度向量再次变换到频域;
- 第二,由于滤波器系数向量后面补了N 个零(参考步骤一),为了保证结果的正确性,梯度向量也需要在后面补N 个零。
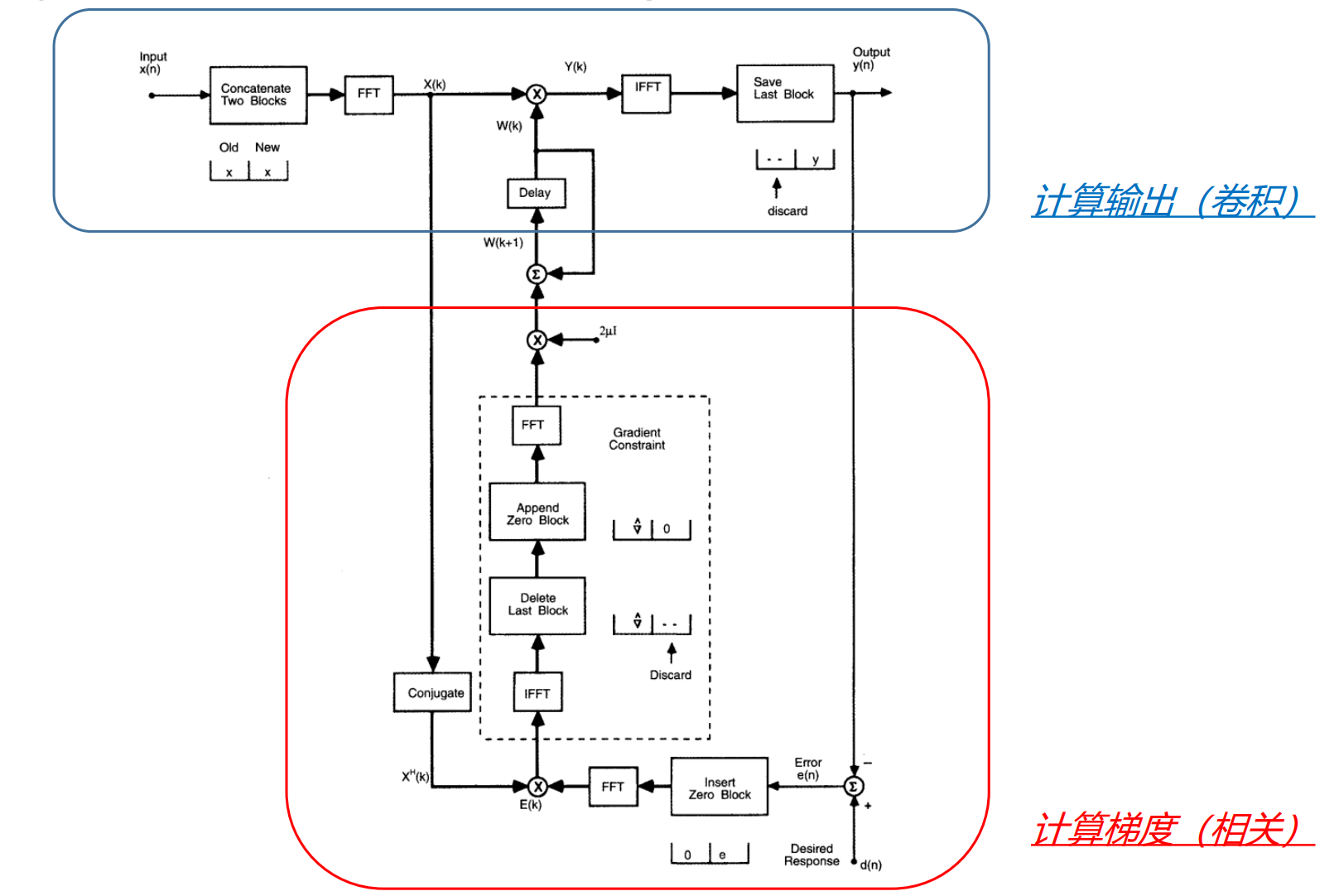
下面是frequency-domain adaptive filtering (FDAF)的总体框架图
可以看出FDAF技术就是在BLMSAF的基础上发展而来,本质上解决的都是同一个问题,即分块条件下的LMS滤波器梯度更新问题。
1.6、关于LMS算法的讨论
LMS算法对输入信号有何种要求?
LMS要求不同时刻输入的向量$\mathbf{x}(n)$线性无关————这是LMS的独立性假设,如果如输入信号存在相关性,会导致前一时刻迭代产生的梯度噪声传播到下一次迭代,造成误差的反复传播,收敛速度慢,跟踪性能变差。
所以理论上,LMS算法对白噪声的效果最好。
对于带有相关噪声的输入信号,如语音信号,有相应的“解相关LMS算法”。
归一化LMS(NLMS),功率归一化LMS(PNLMS )
NLMS
本质上是一个东西,只不过在更新方程中,除以了一个用于归一化的因子$\mathbf{x}^{T}(n) \mathbf{x}(n)$
思想是:对于较大的输入,会导致梯度噪声的放大,因此需要用输入向量的平方范数进行归一化。
PNLMS
功率归一下LMS是NLMS的改进,它对调整步长进行改写,
功率归一化LMS(PNLMS)是利用归一化项 $\mathbf{x}^{T}(n) \mathbf{x}(n)$调整学习速率,数值稳定性要好于NLMS。当$\alpha=1$ 时,PNLMS退化为NLMS。
频域自适应滤波 学习速率的选取
我们在推导频域自适应滤波方法的时候,为了简化问题,将每一个frequency bin上的学习速率均设为常数$\mu$。
在实际工程应用中,用的更多的一种方法是,对第m 个frequency bin,利用输入信号在这个频点的功率$P_m(k)$对学习速率进行归一化:(和时域LMS归一化思想一致)
频点功率$P_m(k)$通常采用迭代的方式求得
关于期望信号$d(n)$
LMS算法中我们已知的有输入信号$x$,和预测输出信号$y$,实际情况下是不知道期望输出的,如果知道了期望输出那么就没有进行滤波的必要了。因此需要用一些方法来估计期望输出, 具体而言,期望输出可以用以下几种方法获取。出处
- 1、使用延迟后的输入信号作为参考信号$d$,即$d(n) = x(n-i)$,其中i为延迟量,可正可负(用于自适应预测)
- 2、期望信号为信号与噪声之和,即$d(n) = x(n) + s(n)$,其中$s(n)$为训练时使用的噪声(用于自适应干扰抵消器,需要噪声与输入信号不相关)
- 3、直接用输出代替期望信号,即$d(n) = x(n)$
- 4、从$x(n)$中估计$d(n)$ ,$d(n) = y(n) + v(n)$,其中$v(n) = w(n)-wo$ ,$wo$是维纳滤波器的最优权值。具体见维纳滤波(感觉很离谱啊,求维纳滤波你也得需要期望信号啊)
其实这一部分在matlab 官方教程 自适应滤波以及应用概述 里面的就有,讲得十分透彻.
二、RLS 滤波器(Recursive Least Square)递归最小二乘算法
2.1、回顾与思路
最小均方误差准则(MMSE)
前面也说过,这种求“期望”的方案非常不好求,与LMS算法一样,RLS也想把期望符号去掉再来更新滤波器系数,而它去期望的方案是把把均方误差改成 求误差的平方和。即
其实,与LMS的代价准则等价,是对所有时刻(所有历史时刻)的误差进行“均匀加权的结果”,也就是无论 某时刻 距离当前时刻的距离有多远,这一时刻对当前评价准则$J(\mathbf{w})$的贡献 权重 是相同的。这也可以称之为“均匀加权函数”
这种均匀加权的策略对于平稳过程当然不错,但是对于语音信号这种非平稳过程就不太友好了。那么就有这样一种想法,既然是非平稳的过程,那么我希望对于里当前时刻越近的时间点,他对评价指标的影响越大,也就是给他的加权越重,反之,越轻。
2.2、新的误差准则
采用指数加权的定义方式,调整目标函数为:
其中,n为“当前时刻”,i为遍历的“历史时刻”,$0<\lambda \leq1$为“遗忘因子”。
遗忘因子的作用是对离 n 时刻越近的误差加比较大的权重,而对离 n 时刻越远的误差加比较小的权
重,也就是说对各个时刻的误差具有一定的遗忘作用。
如果$\lambda=1$表示无任何遗忘功能,或具有无穷记忆功能,此时RLS退化为LS方法。
如果$\lambda->0$表示只有当前时刻的误差起作用,而过去时刻的误差完全被遗忘。
另外 特别注意:
对于误差的定义: 用的是$|e(i)|=\left|d(i)-\mathbf{w}^{T}(n) \mathbf{x}(i)\right|$而不是 $|e(i)|=\left|d(i)-\mathbf{w}^{T}(i) \mathbf{x}(i)\right|$。
通俗点来说就是,对于$i$时刻(先前时刻)的误差,用的是$n$时刻滤波器的系数来估算的,而不是$i$时刻,也就是所谓的“后验误差”。 原因呢是:我们认为 在自适应更新过程中,滤波器总是变得越来越好,这意味着对于任何的 $i<n$, 总认为$\left|d(i)-\mathbf{w}^{T}(n) \mathbf{x}(i)\right|<\left|d(i)-\mathbf{w}^{T}(i) \mathbf{x}(i)\right|$,
这其实是一个比较主观的决定,实际工程当中,采用先验误差还是后验误差差别其实非常小,因为一旦滤波器的系数收敛,采用哪种方式来定义误差差距并不是很大。并且,采用后验误差运算量,占用内存上其实更小一些。
2.3、RLS算法 推导
同样的,让$J_{n}(\mathbf{w})$的对w求导,令梯度为0,得到
其中,
这依然是加权意义下的“维纳解”
此外,对于相关矩阵$\mathbf{R}(n)$与相关向量$\mathbf{r}(n)$有如下递推关系。
看起来只要知道上一时刻的相关矩阵和相关向量,再利用递推公式就能完整地构建改进型的维纳滤波器,步骤如下。
其实,这样的思想是可以,但计算量太大了,计算量主要在于求相关矩阵的逆的过程,每一步都要求,这样计算量太大了。
如果将相关矩阵的逆设为矩阵$\mathbf P(n)=\mathbf R^{-1}(n)$,那么能否直接得到$\mathbf P(n)$矩阵的递推公式,从而避免矩阵求逆的运算呢?
推导如下:
由矩阵求逆引理
现令
就能得到
其中,我们称$\mathbf{k}(n)$为增益向量
ok,我们现在得到了$\mathbf P(n)$的递推公式,那么仅需与相关向量相乘就能得到最优滤波器系数向量了。
即
带进最优滤波器系数向量公式,得到滤波器更新公式 也即RLS算法更新公式:
($ \varepsilon(n)$为先验估计误差误差)
推导过程
中间一步的推导:
2.4、标准RLS算法执行流程
初始化RLS算法执行步骤:
1)初始化:
$\mathbf{w}(0)=\mathbf{0}$、$\mathbf{P}(0)=\delta^{-1}\mathbf{I}$、$\delta$是一个很小的正数,
PS:$\mathbf{P}(0)$的取法有点“讲头”的,首先R(0)是一个相关矩阵,所以是一个对称阵,另外为了方便求逆,所以取单位阵,其次,之前也说了,RLS的误差准则是,离当前时刻越远,其影响对当前时刻越小越好,所以,给他乘一个很小的系数。
2)对于每一个时刻n,重复下面的计算:
$\quad$ 先验误差:$\varepsilon(n)=d(n)-\mathbf{x}^{T}(n) \mathbf{w}(n-1)$
$\quad$ 增益向量:$\mathbf{k}(n)=\frac{\mathbf{P}(n-1) \mathbf{x}(n)}{\lambda+\mathbf{x}^{T}(n) \mathbf{P}(n-1) \mathbf{x}(n)}$
$\quad$ 逆矩阵更新: $\mathbf{P}(n)=\frac{1}{\lambda}\left[\mathbf{P}(n-1)-\mathbf{k}(n) \mathbf{x}^{T}(n) \mathbf{P}(n-1)\right]$
$\quad$ 滤波器更新:$\mathbf{w}(n)=\mathbf{w}(n-1)+\mathbf{k}(n) \varepsilon(n)$
代码实现
function [y,e,w]=MyRLS(L,lambda,x,d)
% 输入参数
% L 滤波器阶数
% lambda 遗忘因子; lambda=1,表示“不遗忘”,等价于LS ,Lambda=0表示除了当前,全部遗忘 默认 lambda=0.98
% x 输入信号; 是指 直接进入滤波器于滤波器系数相卷积的那一路
% d 期望信号:是指 不进入滤波器,而只作为“参考”,产生误差信号的那一路
% output 输出:是指滤波器的直接输出
% w 滤波器系数:
% 注意 输入信号于期望 输入应该保证一样长
N=length(d); % 总输入长度
% 初始化
w = zeros(1,L); % 行向量
delta=0.001;
P=1/delta*eye(L,L) ; % 初始化的 相关矩阵的逆矩阵
e=zeros(1,N);
y=zeros(1,N);
k=zeros(1,L);
x = [zeros(1,L -1) x']; % 行向量
for n = 1:N % 每一个采样点“前进一步”
m = n + L -1; % n是“起始点”,m则是“结束点”
xpad = x(m-L+1:1:m)'; % 列向量 :
%关于x是否应该“翻褶”这一点已经在LMS 那个程序里面 说过一遍,结论就是:只要对应好,就没必要翻褶,但是输出的w应该是倒序输出
y(n) = w*(xpad); % 滤波器输出 y=w*x
e(n) = d(n) - y(n); % 误差信号 e=d-y 是一个数
% 求增益向量
%k=P*xpad/(lambda+xpad'*R*xpad) 这一步由于 求 了两次 P*xpad,可以优化为
k=P*xpad;
k=k/(lambda+xpad'*k); % 列向量
% 更新逆矩阵
P=(P-k*xpad'*P)/lamda;
% 滤波器系数更新
w = w + k'* e(n);
end
end
2.5 RLS 与LMS 对比
一个广泛的共识是,RLS算法的收敛速度和跟踪性能都优于LMS算法,所付出的代价是需要
更复杂的计算。
| 算法 | LMS | RLS |
|---|---|---|
| 计算误差 | 后验误差 | 先验误差 |
| 收敛速度 | 慢 | 快 |
| 跟踪性能 | 慢 | 快 |
| 计算代价 | 小 | 大 |
另外,由于RLS使用了自相关矩阵的逆矩阵的递推,所以,一旦输入信号的自相关矩阵接近奇异时(输入信号各个时刻不要“太相关”),RLS的收敛速度和跟踪性能会严重恶化。
可以看到,LMS 算法 与RLS 算法 在各个方面走了两个极端,下面要讲的 仿射投影算法可以说是两种“极端”的折中,也可以说是包含二者的一种统一框架。
三、APA(Affine Projection algorithm)仿射投影算法
3.1、再次从一个N阶系统$\mathbf{w(n)}$出发…(新的框架)
考虑一个N阶系统$w(n)$ ,
这一次我们将构造一个更加通用的模型,首先输入、输出、权重 都可以是复数
N阶系统(n阶滤波器)n时刻的滤波器系数为,
如果将 滤波器原本滤波器当前的输出扩展成一组向量 。向量内容 为滤波器最近的L个输出为:
那么,相应的输入也得改变,将是一个矩阵 N*L的矩阵,
从原来的
扩展为
也即,展开来写
平行于斜对角线元素的行相等
这是一个广义上的Hankel 矩阵,可以看看 matlab 教程,注意与 toplize矩阵相区分。
此时滤波器输出变成了
3.2、滤波器更新策略?
若令滤波器更新公式为:
将更新后的滤波器系数带入到滤波器输出公式当中
公式的前一项是当前输入矩阵进入前一时刻滤波器输出的结果,这肯定与当前时刻滤波器有一定误差,我们将第二项整体 定义为“先验误差向量”,
由于$\mu$仅仅是一个可变的“学习率”,对结构来说并不太重要,我们将其简化 令其等于1,也即$\mathbf{e}(n)=\mathbf{X}^{T}(n) \Delta \mathbf{w}_{n}^{*}$ 或
可以发现 这种形式与线性代数中学到的线性方程组($\mathbf{A}\mathbf{x}=\mathbf{b}$)一致,它由L个(行)N元线性方程决定。
而这个线性方程组的解(即$ \Delta \mathbf{w}_{n}$),就是我们想要的“滤波器更新策略”,那么只要求解这个N元方程组即可得到更新策略了。
补充知识(求解线性方程组的相关背景知识):
对于线性方程组:$\mathbf{A}_{m\times n}\mathbf{x}_{n \times 1}=\mathbf{b}_{m \times 1}$
只考虑行满秩的情况下:
1):$m=n$,则是唯一解,而且是精确解
2):$m<n$, 方程数小于未知数个数,也叫欠定方程组 ,将有无穷解(有$n-rank(A)$个解系)(可以将每一个方程理解为一个约束条件,那么约束条件越少,解(解系)“越多”)。但是我们为了得到一个确定的解,添加一些约束条件,在$\mathbf{x}$的范数最小,也即$min{\{norm(\mathbf{x})\}}$ 的这一约束下 有唯一解,叫做“最小范数解”可以把$\mathbf{A}^{H}(\mathbf{A}\mathbf{A}^{H})^{-1}$ 视为$\mathbf{A}$ 的‘逆矩阵’,只不过这个矩阵作用在$\mathbf{A}$ 的左边。即$\mathbf{A}\mathbf{A}^{H}(\mathbf{A}\mathbf{A}^{H})^{-1}=\mathbf{E} $
3):$m>n$, 方程数大于未知数个数,也叫超定方程组,线性代数理论中是无解的,更进一步扩展的话只能叫“没有精确解”,事实上,我们可以找到一个近似的解,让等式两边的误差平方尽可能的小,也即最小化$min{\{norm(\mathbf{Ax-b})\}}$条件下,即”最小二乘解“可以把$(\mathbf{A}\mathbf{A}^{H})^{-1}\mathbf{A}^{H}$ 视为$\mathbf{A}$ 的‘逆矩阵’,只不过这个矩阵作用在$\mathbf{A}$ 的右边。即$(\mathbf{A}\mathbf{A}^{H})^{-1}\mathbf{A}\mathbf{A}^{H}=\mathbf{E} $
在矩阵论当中,这些逆矩阵可以有一个统一的称呼 叫做“广义逆矩阵” 合并写为$\mathbf{A}^{\dagger}$,
那么,矩阵的解可以统一写为
根据上述线性方程组的结论,重新审视方程$\mathbf{X}^{H}(n) \Delta \mathbf{w}_{n}=\mathbf{e}^*(n)$
情况一:当,$1\leq L <N $,方程数小于未知数,方程为欠定方程组,具有唯一最小范数解:
此时,自适应算法变为:
当$L=1$时,将退化为NLMS算法,即
对比上面的NLMS 只是学习率有有变化,其实没有本质上的区别。
实际当中,对于这种方程,L一般取2、3就足够了。情况二: 当$L \geq N$s时,方程数大于为质数个数,方程为超定方程,具有唯一最小二乘解:
此时,自适应算法变为:
如果我们令$\mu=1$ , $\mathbf{R}(n)=\frac{1}{L} \mathbf{X}(n) \mathbf{X}^{H}(n) $, $\mathbf{r}(n)=\frac{1}{L} \mathbf{X}(n) \mathbf{y}^{}(n)$, 并结合等式 $ \mathbf{e}(n)=\mu \mathbf{X}^{T}(n) \Delta \mathbf{w}_{n}^{}=\mathbf{y}(n)-\mathbf{X}^{T}(n) \mathbf{w}^{*}(n-1) $ ,可得:
等价于RLS(递推最小二乘算法)(PS:RLS算法中$\mathbf{w}(n)=\mathbf{R}^{-1}(n) \mathbf{r}(n) $,相当于省略了所有的$\mathbf{w}(n-1)$项)
代码实现
function [y,e,w]=MyAPA(L,P,x,d)
% 输入参数:
% L:滤波器阶数
% P: 重用次数
% x;输入信号
% d:期望信号
% 输出参数:
% y:输出信号
% e:误差信号
% w: 滤波器系数
% 注意 输入信号于期望 输入应该保证一样长
N=length(d); % 总输入长度
% 初始化
w = zeros(1,L); % 行向量
e=zeros(1,N);
y=zeros(1,N);
k=zeros(1,L);
Y=zeros(1,p)
x = [zeros(1,L +P-2) x']; % 行向量
d = [zeros(1,P- 1) d'];
for n = 1:N % 每一个采样点“前进一步”
m = n + L + P -2; % n是“起始点”,m则是“结束点”
Xpad = hankel(x(n:1:(n+L-1)),x((n+L-1):1:m)); % 输入矩阵, L*P列
% 关于 时序问题,可以意LMS的代码为例,看看是否正确
ypad=conj(w)*Xpad; % 行向量 1*P 与x 一样 与定义的时序相反
dpad=d(n:1:(n+P-1)); % 行向量
epad=ypad-dpad; % 误差 e=d-y 是一个向量
% 求
% 求增益向量
%k=P*xpad/(lambda+xpad'*R*xpad) 这一步由于 求 了两次 P*xpad,可以优化为
k=P*xpad;
k=k/(lambda+xpad'*k); % 列向量
% 更新逆矩阵
P=(P-k*xpad'*P)/lamda;
% 滤波器系数更新
w = w + k'* e(n);
end
end
AP算法:
- 仿射投影算法提供了一套自适应滤波分析的统一框架,这套框架将LMS、AP、RLS三种算
法串联在一起。 - AP算法是计算复杂度和性能介于LMS和RLS之间的自适应算法,在AEC、multi-channel等
场景中都有应用。可以根据实际项目中对计算复杂度、收敛速度的要求,选择合适的自适应算法,解决
自身场景的问题。 - 其实RLS、AP算法都有各自的快速算法,可以提高收敛速度或减少计算量
总结:
- 维纳滤波:
平稳环境、最小均方意义下的统计最优滤波器,理论意义大于实际意义。而且他并非自适应滤波器算法(不会动态跟踪),因为它整体意义下的最优(要 求 一系列期望) - 最小均方(族)自适应滤波器
- LMS滤波器 (标准LMS)
- 分块LMS滤波器 BLMS
- 归一化LMS滤波器 NLMS
- 频域自适应滤波器 FDAF
- 子带自适应滤波器
- 等等
- 递归最小二乘(族)自适应滤波器
- RLS滤波器,收敛速度更快,但是计算复杂度高
- 放射投影自适应滤波器
- 各种性能介于以上二者之间,更重要的,它提供了一个统一的框架
补充,自适应滤波“家族”其实还有一个重要成员,卡尔曼滤波器, 它是一种基于状态转移原理的一种滤波器,并且,RLS算法滤波器也可以视为 卡尔曼滤波器的一种具体实现形式。