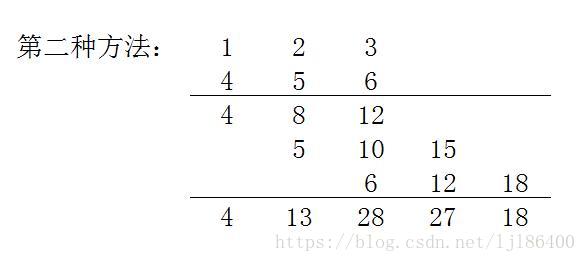2、DSP基础

2.1 DSP 基本运算

模拟数据——》采样——》量化——》编码——》数字信号

线性卷积（ linear convolution）

$y(n)=\sum_{m=-\infty}^{\infty} x(m) h(n-m)=x(n) * h(n)$

卷积的计算方法

卷积在按照定义计算可分为四步：翻褶、移位、相乘、相加

第二种方法比较简单但不太推荐
如下：

在数字信号处理当中信号通过一个线性时不变系统被抽象为一个卷积操作

圆周移位（circular shift）

等价于经过周期延拓，平移后加窗

圆周卷积（circular convolution）

如果$x_1(n)$和$x_2(n)$ 都是长度为N的有限长序列
$X_1(k)=\operatorname{DFT}\left[x_{1}(n)\right] \quad X_{2}(k)=\operatorname{DFT}\left[x_{2}(n)\right]$
且 $Y(k)=X_{1}(k) X_{2}(k)$
那么 $\begin{aligned} y(n)=\operatorname{IDFT}[Y(k)] &=\left[\sum_{m=0}^{N-1} x_{1}(m) x_{2}((n-m))_{N}\right] R_{N}(n) \\ &=\left[\sum_{m=0}^{N-1} x_{2}(m) x_{1}((n-m))_{N}\right] R_{N}(n) \end{aligned}$ 定义为$x_1(n)$和$x_2(n)$的圆周卷积。

从定义也可以看出DSP种那个经典的结论：时域上的卷积为频域的乘积，这里的卷积是指圆周卷积操作！！

注意：与线性卷积相比，圆周卷积多了周期延拓和取主值序列两个步骤。因此必须指定圆周卷积的点数N。
N也叫主值区间，做圆周卷积时，这个参数时必要的

由于卷积运算相当复杂，所以当数据比较长时求卷积的操作等价于：先将两个输入数据分别求DFT转到频域在相乘，再IDFT 转到时域，这样来求卷积，大大减少时域卷积的运算量。

但是一般我们要的是线性卷积的结果，怎么通过圆周卷积求线性卷积呢？发现当做N2点的圆周卷积时，N1>=N2时，圆周卷积的后N1-N2+1个点与线性卷积相同，可以通过补零的操作转换。

线性相关（liear correlation）

$r_{x y}(m)=\sum_{n=-\infty}^{\infty} x(n) y^{*}(n-m)$

相比于卷积的式子：少了翻褶的操作，淡多了一个求共轭的操作

圆周相关（circular correlation）

前面与圆周卷积条件相同
如果$R_{x y}(k)=X(k) Y^{}(k)$
$r_{x y}(m)=I D F T\left[R_{x y}(k)\right]=\sum_{n=0}^{N-1} y^{}(n) x((n+m))_{N} R_{N}(m)=\sum_{n=0}^{N-1} x(n) y^{*}((n-m))_{N} R_{N}(m)$
称$r_{x y}(m)$是$x(n)$和$y(n)$的圆周相关。

圆周相关与线性相关关系
一般的，如果两个有限长序列的长度为N和 N2，且满足N≥ N2，则有圆周相关的前N-N2＋1个点，与线性相关的结果一致。（因为少了翻褶操作）

补充

卷积神经网络卷积
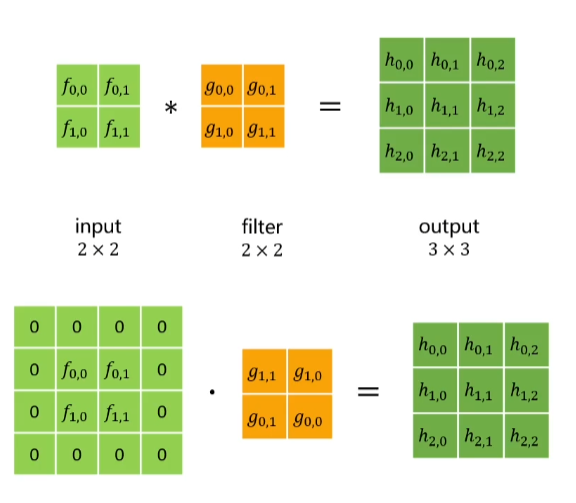
二维卷积：
$h(i, j)=\sum_{u} \sum_{v} f(u, v) g(i-u, j-v)$

举例来说就是
f是输入二维的数据，g是卷积核
$f=\left[\begin{array}{ll}f_{0,0} & f_{0,1} \\ f_{1,0} & f_{1,1}\end{array}\right]
\quad g=\left[\begin{array}{ll}g_{0,0} & g_{0,1} \\ g_{1,0} & g_{1,1}\end{array}\right]$

二维卷积举例

步骤就是

先把输入的f矩阵扩展，扩展大小根据g决定，如g是一个N*M的阵，上（下）层就多N-1行，左右就多M-1列，填零。
把g矩阵按各个维度翻转（如果不翻转就是二维的互相关操作）
做类似于互相关（对应元素相乘再相加）的操作
- $h_{0,0}=0g_{1,1}+0g_{1,0}+0g_{0,1}+f_{0,0}g_{0,0}$
- $h_{0,1}=0g_{1,1}+0g_{1,0}+f_{0,0}g_{0,1}+f_{0,1}g_{0,0}$
- ……

彩色图片有R（red）G（green）B（blue）三个通道，每个通道取值为[0-255]
灰度图片与RGB换算关系: $gray=R0.299+G0.587+B*0.114$

二维卷积应用举例：
Prewitt算法的边缘检测

步骤一、获取卷积核
- 横向边缘检测卷积核
  $f1=\left[\begin{array} {} 1 & 1 & 1 \\ 0 & 0 & 0 \\ -1&-1&-1\end{array}\right]$
  与他做卷积相当于上下两行（隔一行）做差，
- 同理可得横向边缘卷积核
  $f2=\left[\begin{array} {} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1&0&-1\end{array}\right]$
步骤二：将图像分别与卷积核做卷积假设得到 G 和G’
步骤三：将G与G’各个元素做取绝对值得到|G| |G’|
步骤四：最终用$P(x,y)=max\{ |G(x,y)| ,|G’(x,y)|\}$ 得到边缘检测图

此外：CNN中的卷积，在前向传播时采用与卷积核的互相关，反向误差传播采用二维卷积

2.2、采样定理

时域采样等价于频域上的对信号的周期延拓，延拓周期为$f_s=\frac{1}{T}$
(以$\Omega$为单位时，延拓周期是$\Omega_s=\frac{2\pi}{T}$)
著名的奈奎斯特采样频率：能无失真恢复的条件：采样频域大于信号最高频率的两倍

采样定理的推导

采样信号可以视为原始信号与周期冲击信号的乘积

$\hat{x}_{a}(t)=x_{a}(t) \cdot \delta_{T}(t)$

等式两端取DTFT

$\hat{X}_{a}(j \Omega)=\frac{1}{2 \pi}\left[\Delta_{T}(j \Omega) * X_{a}(j \Omega)\right]=\frac{1}{T} \sum_{k=-\infty}^{\infty} X_{a}\left(j\left(\Omega-k \Omega_{s}\right)\right)$

这一步的推导见下面
首先要求$\delta_{T}(t)$的傅里叶变换是什么，在离散域就是DTFT，
由于$\delta_{T}(t)$是周期信号，那么他在时域上就可以写成傅里叶级数的形式：

$\delta_{T}(t)=\sum_{k=-\infty}^{\infty} A_{k} e^{j k \Omega_{s} t}$
其中 $A_{k}$ 响应频率波的幅度、$\Omega_{s}$ 是采样频率
$\begin{aligned} A_{k} &=\frac{1}{T} \int_{T} \delta_{T}(t) e^{-j k \Omega_{s} t} d t=\frac{1}{T} \int_{T} \sum_{m=-\infty}^{\infty} \delta(t-m T) e^{-j k \Omega_{s} t} d t \\ &=\frac{1}{T} \int_{T} \delta(t) e^{-j k \Omega_{s} t} d t=\frac{1}{T} \end{aligned}$ 倒数第二个等号：因为在一个周期内，只有一个冲激信号

那么对$\delta_{T}(t)$的 DTFT 相当于对$\delta_{T}(t)=\frac{1}{T} \sum_{k=-\infty}^{\infty} e^{j k \Omega_{s} t}$求DTFT
而$DTFT\{e^{j k \Omega_{s} t}\}=2\pi\delta(j（\Omega-k\Omega_s）)$
所以 $DTFT\{\delta_{T}(t)\}=\frac{2\pi}{T}\sum_{k=-\infty}^{\infty}\delta(j（\Omega-k\Omega_s）)$
将此结果与$X_{a}(j \Omega)$ 做卷积就可以得到上式采样定理的结果

对于一个16kHz 的语音数据，将其降采样到8kHz

采用抽取的方式降采样
但是抽取前一定要通过一个抗混叠滤波器（因为降采样会频谱会扩展，有可能发生频谱混叠）举例

采样定理的延申——“空域采样定理”
| 时域 | 空域 |
| —— | —— |
| 时域采样序列（冲击函数序列） | 麦克风阵列 |
| 采样率$fs$ | 麦克风之间的间距$d$ |
| 信号的最高频率 $fh$ | 信号最小波长$\lambda_{min}$ |
| $fs>2f_h $采样定理 | $d<\lambda_{min}/2$ 也叫半波长理论|

傅里叶变换

傅里叶级数

本质上可以视为把一个周期信号用一系列正弦余弦波表示，整数倍频率的正弦余弦波可以视为一组标准正交基，正交基的系数可以通过”相关操作”（或者说内积的方式）求得

$x(t)=\sum_{k=-\infty}^{\infty} X\left(j k \Omega_{0}\right) e^{j k \Omega_{0} t}$

这里说的系数$X\left(j k \Omega_{0}\right)$系数(相当于上一小节采样定理推导中的$A_k$，当信号定下来以后只与$k$有关)通过下式求得:

$X\left(j k \Omega_{0}\right)=\frac{1}{T_{0}} \int_{-T_{0} / 2}^{T_{0} / 2} x(t) e^{-j k \Omega_{0} t} d t$$，可以看到本质上就是通过一个周期内**信号**与**正交基**的相关（内积）操作，来”抽取“对应频率的数据。 **傅里叶级数说明：周期信号对应的是离散谱**，仅在频率为符号频率的整数倍上有值，这里所求的系数就是离散谱上每个整数倍周期的幅度，以及相位。 #### 连续傅里叶变换将周期信号的傅里叶级数的周期拓宽之周期无穷大变成非周期信号，傅里叶级数就变成了连续傅里叶变换 $$X(j \Omega)=\int_{-\infty}^{\infty} x(t) e^{-j \Omega t} d t$ $x(t)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} X(j \Omega) e^{j \Omega t} d \Omega$

第一个式子就相当于求上一小节傅里叶级数的系数的公式意义上：仍然是通过内积的方式，“抽取”对应频率分量的系数。

与傅里叶级数不同的是，由于时域信号非周期，因此频域中是连续谱

离散时间傅里叶变换（DTFT）

离散非周期信号x(n)的DTFT可以表示为：

$X\left(e^{j \omega}\right)=\sum_{n=-\infty}^{\infty} x(n) e^{-j \omega n}$ $x(n)=\frac{1}{2 \pi} \int_{-\pi}^{\pi} X\left(e^{j \omega}\right) e^{j \omega n} d \omega$

注意，这里不再采用模拟频率中的大写$\Omega$,而是采用小写的$\omega=2\pi$,
因为在连续信号是不涉及采样的
$\Omega=2\pi f=2\pi/T$ 一般不会写成$\Omega=2\pi f_s=2\pi/T_s$ ,因为f 或者T 是连续信号本身的属性，不是采样频率，或者采样周期。

连续信号经过采样后变成了离散信号，所以 离散（采样）信号本身是带有采样频率这一隐藏属性 故采用归一化的频率$\omega=\Omega/f_s=2\pi f/f_s$ $f$是信号本身的频率，根据采样定律，信号本身最高频率不能超过采样频率的一半（否则就有混叠），所以$\omega$的取值范围只能是{[$-\pi$,$\pi$]. 所以研究数字信号的频域的时候只用研究[$-\pi$,$\pi$]即可。（很容易得$X\left(e^{j \omega}\right)$s是一个周期为$2\pi$的函数，其他周期都是[$-\pi$,$\pi$]的周期延拓）

PS：DTFT 与傅里叶级数形式上非常像，其实这两个就是一对正反变换

离散傅里叶变换 DFT

也叫时间离散、频域离散的傅里叶变换
与DTFT的区别就是将 DTFT研究的非周期信号改为研究周期信号，频域变成了离散信号

$\begin{aligned} &X(k)=\sum_{n=0}^{N-1} x(n) e^{-j \frac{2 \pi}{N} n k}=\sum_{n=0}^{N-1} x(n) W_{N}^{n k} \\ &x(n)=\frac{1}{N} \sum_{k=0}^{N-1} X(k) e^{j \frac{2 \pi}{N} n k}=\frac{1}{N} \sum_{k=0}^{N-1} X(k) W_{n}^{-n k} \end{aligned} \quad W_{N}=e^{-j \frac{2 \pi}{N}}$

DFT针对有限长信号或者周期信号
DFT相当于对DTFT中的正变换加以采样，造成时域信号的周期性，因此时域信号应限制在一个周期内。凡是用到离散傅里叶变换的时候，有限长序列都是作为周期序列的一个周期来表示的，都隐含有周期性意义。

总结：
一个域上的离散性对应另一个域的周期性
一个域上的周期性对应另一个域的离散性

离散傅里叶变换也可以用矩阵来表示

$\mathbf{F}=\left[\begin{array}{ccccc}1 & 1 & 1 & \ldots & 1 \\ 1 & W_{N} & W_{N}^{2} & \cdots & W_{N}^{N-1} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & W_{N}^{N-1} & W_{N}^{2(N-1)} & \cdots & W_{N}^{(N-1)(N-1)}\end{array}\right] \quad W_{N}=e^{-j \frac{2 \pi}{N}}$ $\mathbf{F}^{H} \mathbf{F}=\mathbf{F F}^{H}=N \mathbf{I} \quad \quad \mathbf{F}^{-1}=\frac{1}{N}\mathbf{F}^{H}$

那么DFT以及IDFT可以表示为

$\mathbf{X}(k)=\mathbf{F} \mathbf{x}(n)$ $\mathbf{x}(n)=\mathbf{F}^{-1}\mathbf{X}(k)$

总结

注意：

面对四种傅里叶变换时，要用一种”抽取”的思想看待所有公式，
离散、周期的关系

2.3、傅里叶变换的几个问题

频谱泄露

频谱泄漏是指由于信号截断造成的原始信号频谱扩散现象。

产生频谱泄漏的原因是对信号的截断。信号的截断相当于在原始信号z(n)与一个窗函数u(n)相乘，在频域中相当于各自频谱的卷积过程。卷积的结果造成原始信号频谱的“扩散”(或拖尾、变宽），这就是频谱泄漏。

加窗是因为DFT只能对有限长或者说周期信号进行变换，对于后者还具体分为周期截断和非周期截断，非周期阶段会造成频谱泄露，可以采用不同的窗函数来缓解频谱的泄露

所以在对语音信号分帧加窗的过程中避免使用频域拖尾严重的窗函数，采用如汉明窗之类的窗函数：
$w_{r e c}(n)=R_{N}(n)$
$w_{\text {hamming }}(n)=\left[0.54-0.46 \cos \left(\frac{2 \pi n}{N-1}\right)\right] R_{N}(n)$