离散傅里叶变换 DFT

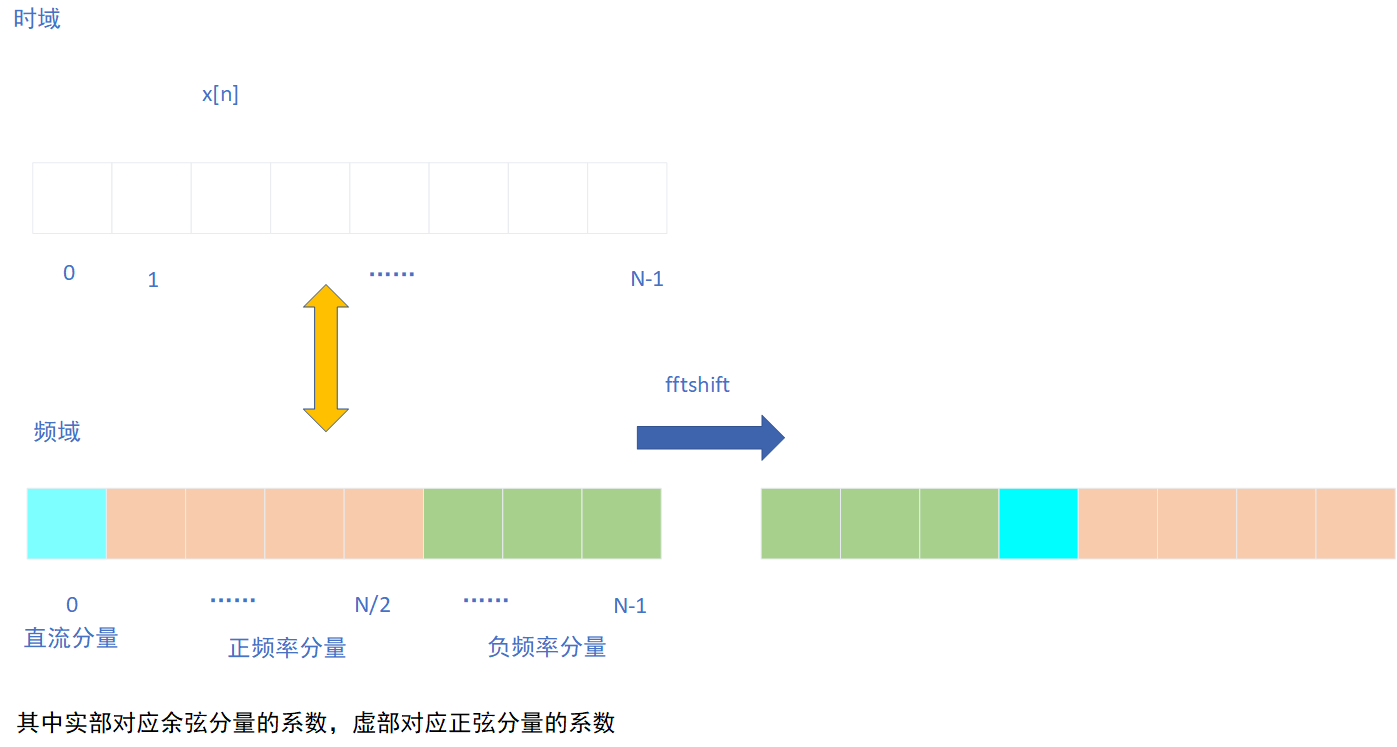
离散傅里叶变换（DFT）是离散信号时/频域变换的方法。作用类似于棱镜，将由多种频率混合而成的语音按频谱散射，经过种种处理后，再反变换到时域，就可以获得“提纯”后的语音信号。实数DFT的输入是实数，得到的频点有两个集合，分别是正弦（cos）和余弦（sin)函数的系数，对应于正频分量和负频分量。

$\begin{aligned} &\mathrm{X}(k)=\sum_{n=0}^{N-1} x(n) e^{-j \frac{2 \pi k n}{N}}, k=0, \ldots \ldots N-1 \\ &\mathrm{X}_{r e}(k)=\sum_{n=0}^{N-1} x(n) \cos \left(\frac{2 \pi k n}{N}\right), k=0, \ldots \ldots N-1 \\ &\mathrm{X}_{im}(k)=\sum_{n=0}^{N-1} x(n) \sin \left(\frac{2 \pi k n}{N}\right), k=0, \ldots \ldots N-1 \end{aligned}$

短时傅里叶变换STFT

为什么分段（帧）处理？

原因：
- 1、时序原因，频谱图是无法得到有关于时间先后的信息的，比如说“ai”这个字的发音，“a”和“i”的发音在时间上是有顺序关系的，这时可以将序列等时分割成若干个小段，按顺序对每一个小段做DFT分析，先得到“a”的谱，后得到“a”到“i”的谱，最后是“i”的谱。
- 2、实际中的语音信号往往是实时的数据流，或者非常长。需要考虑时效性、以及计算量
短时傅里叶变换常用于序列较长或时间分辨率较高的场景，语音信号是时变的，每秒产生约10个音节，在10~30ms时长内的语音信号可以看成是准静态的。下面的流程图展示了STFT的分析和综合处理流程为

graph TD
A[原始信号] --> B(加重叠窗 汉明窗 汉宁窗 凯撒窗 得到加窗的重叠的分段信号)
    B --> C[FFT]
    C --> D[频域分析处理]
    D --> E[IFFT]
    E --> F[分段逆变换]
    F --> G[合成]

流程图再分段的过程中采用了加窗操作，而且加窗分段时时域有叠加。
这是为什么呢？

为什么加窗（把矩形窗换成其他窗）

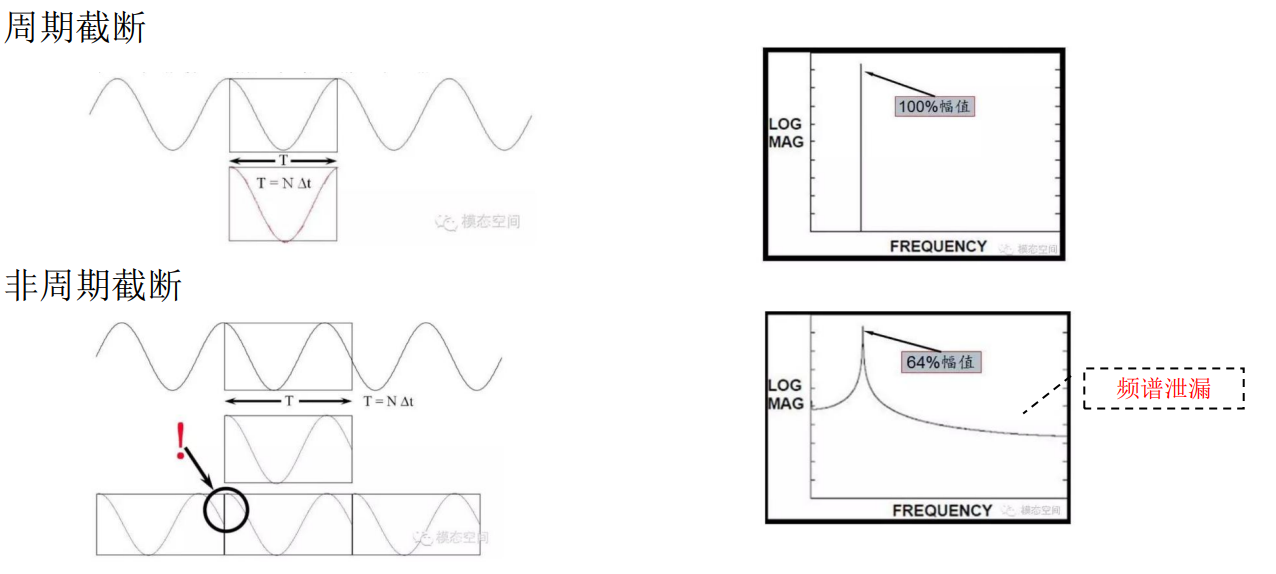
首先，如果采用了直接分段的方案，做STFT，每一段分别做FFT（FFT点数为窗函数长度），根据FFT定义，相当于对这一份分段进行周期延拓形成一个无限长的周期信号。如果截取窗的长度对于信号中的某一个频率分量不是其周期的整数倍，那就会产生新的频域分量(如下图，在截断处产生了“虚假的峰值”，也就产生了新的频域分量)，造成严重的频谱泄露和混叠（这个频域的能量会弥散到周围其他频域当中，此频点能量降低，如果能量够大甚至会淹没其他频率点）。
其次如果直接从频域上看，相当于信号频谱与Sa函数相卷积，把信号频域想象成一个在数个频点上有冲击“信号”，Sa函数与冲激信号进行卷积，相当于对这个Sa函数的移位。进行FFT变换得到的各个系数就是在频域分辨率的整数倍周期（$k/fs$）上进行采样的采样值。那么显而易见，只有满足频点位于这些整数分辨率的频点上的冲击经过与Sa函数的卷积，才不会对其他的频域采样点产生影响（Sa（sinc）函数的自变量除0外，在整数倍pi（整数）处为零点，旁瓣衰减是按照自变量的倒数的一次方进行衰减），也就是发生泄漏。实际信号的很多就落在这些非整数分辨率的频点上（因为信号不只是在时域上来连续，在频域上也是连续的），所以必然会产生频谱泄露，那么，如果泄露时必然的，还可以将Sa函数改为一些旁瓣衰减比较块的函数，其时域就对应着不同的窗，这也就是加窗（把矩形窗换成其他窗）的原因。

为什么叠加？

因为上述流程采用了类似于 OLA 的算法（WOLA）来增加计算精度。下面来介绍一下

重叠保留法（OLS）、重叠相加法（OLA）

OLS 和 OLA 是计算无限长序列（或是长序列）与较短序列卷积或者相关的方案。将时域原本$O(n^2)$ 得计算量转化为频域 $O(nlogn)$的计算量。

区别，OLA精度较高，而且绝大多数情况下都用OLA。OLS 计算量稍小。

OLA计算步骤

输入长序列 x(1:Nx) ,长度 Nx，序列分块长度 L xk(kL+1: min(Nx，(k+1)L)); 短序列 h(1:M)
因为要做 M+L-1=N 点数的DFT（FFT），所以一般选取合适的参数L、M 使得N 等于2的幂次

输入参数：输入长序列x，短序列h，分块长度L
1、计算短序列h的FFT H //不够N长的部分补零，后面补零
2、遍历每一个分块
- 2.1、计算分块的FFT Xk //不够N长的部分补零，后面补零
- 2.2、H Xk 对应位相乘得Yk，求IFFT 得yk
- 2.3、重叠相加（由于 N>M 所以有重叠部分）
3、输出y

OLS 计算步骤
参数与上面一致

输入参数：输入长序列x，短序列h，分块长度L
计算短序列h的FFT H //不够N长的部分补零，后面补零
遍历每一个分块
- 计算分块的FFT Xk //不够N长的取前面该输入序列前面得 N-L位，如果是第一块，前面取零
- H Xk 对应位相乘，求IFFT 得yk
- 去掉yk 前 N-M 位数据
整合输出 y

WOLA （加权OLA）

计算步骤与OLA相差不大，

输入参数：输入长序列x，短序列h，分块长度L
1、计算短序列h的FFT H //不够N长的部分补零，后面补零
2、遍历每一个分块
- 2.0、分块采用窗函数对应位加权
- 2.1、计算分块的FFT Xk //不够N长的部分补零，后面补零
- 2.2、H Xk 对应位相乘得Yk，求IFFT 得yk
- 2.2 plus 、用综合窗对yk 加权
- 2.3、重叠相加（由于 N>M 所以有重叠部分）
3、输出y

下段转自一篇博客地址
虽然加窗能减少频谱泄露，但是加窗也存在一个问题：加窗衰减了每帧信号的能量，特别是边界处。为了解决这一个问题，就引入了合成窗（综合窗）的概念。

在iSTFT中，合成窗是在iFFT之后，对时域信号做的。此次加窗，并不是为了减少频谱泄露，因为之后不再做FFT，不需要满足周期性序列条件。而是为解决分析窗导致能量衰减问题的。为了补回能量，就要考虑到overlap满足一定的条件，即完美重建准则：

$\Sigma_{n=0}^{N-1} h_{a}\left(t-t_{0}-n M\right) h_{s}\left(t-t_{0}-n M\right)=1$

ha为分析窗(analysis window)，hs为合成窗(synthesis windows)。t0为每一帧的第一个采样点，M是hop size，n是第几帧。t当前采样点。

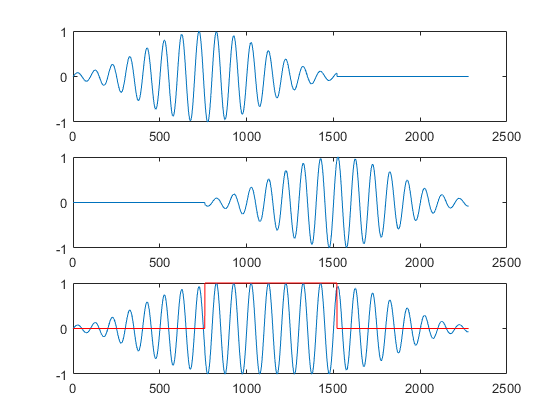
下面用一个例子阐述合成窗是如何重建信号的。下图是一个时域转频域加窗的过程。

. 可以看到，经过加窗后，能量有所衰减。加一个合成窗，且overlap-add，便可以补回能量。如下图所示

. 可以定性看到，在经过overlap，边界处的信号补回原始幅度了。很多修正后的窗如修正巴特沃斯窗、凯撒窗都可以用到WOLA当中。需要注意的是，不同窗具有的最优重叠长度不一样，如Blackman-Harris 窗最优位66.1% ，此处是比较巧妙，分析窗用hamming窗，overlap采用50%，则在合成的时候，就不需要额外加窗了，直接overlap-add就好。

PS：这一块有点类似于通信原理学的残留边带调制VSB 所需要的残留边带滤波器（频域）

一般来说，根据完美重建公式，合成窗的选择，不仅跟分析窗有关，还和overlap有关。不同的overlap要采用不同的合成窗。

音频处理常用概念或算法

下面这几个书中都是一两页介绍带过，很难读透
滤波器组

功能：滤波器组将输入信号分解到多个频带，并对各个频带进行处理，最后将处理完的各个频带组合在一起得到最终的输出。
代码还没看懂，是webrtc 中的代码

混合高斯模型
没看懂

HMM 模型
没懂，但这个应该很重要，后面写博客有机会补充

卡尔曼滤波
不懂

发声机理器件

语音产生机理

（1）语音具有短时平稳性，这是很多语音算法前提之一。
（2）语音发音可以分为清音和浊音两类，发浊音时大部分能量集中在低频段，且在时域上具有周期性，在频域上频谱分布具有共振峰结构。清音和白噪声类似，没有明显的时域和频域特征。
（3) 浊音比如元音的语音产生机理如下：
空气通过正常呼吸进入肺部，进入时一般无语音产生。
空气通过气管排出肺时，依据贝努利定律（在一个流体系统，比如气流、水流中，流速越快，流体产生的压就越小），被声门开口处空气压力拉紧的喉头处的声带会振动。空气流被声门孔的打开和关闭形成了准周期的脉冲。通过咽、口和鼻道时，这些脉冲被频率整形。不同发音器官（颚、舌）的位置决定了产生的声音。
（4）声道气流来源于声带，其作用类似于线性滤波器，对输入波形进行频谱整形，从而发出不同的声音。声道的共振产生共振峰，产生共振的频率称为共振频率，共振的基频由声带决定

发声可以简单看成是激励源信号作用于线性滤波器（IIR）产生的，声道角色可以看成是对输入波形进行频谱整形的线性滤波器，声带提供了声道激励的来源，激励根据声带所处的状态可以是周期性的，也可以是非周期性的。

发生模型

对于从嘴唇最终发出的声音的z变换可以表示为声门$G(z)$、声道$V(z)$和唇激励$R(z)$的积，
为

$X(z)=G(z)V(z)R(z)$

对于非语音输出

$X(z)=N(z)V(z)R(z)$

声道的滤波器系数取决于声道的形状，当激励信号为周期性脉冲，发出原因，当激励信号于噪声接近发出辅音。

这一部分可以看看《语音信号处理第三版》（赵力）第二章，写得更详细