概念解读：

AEC：
声学回声消除，设备自身的（回声）干扰，这会对设备的声音识别等有干扰

NS :
去除背景噪音，特别是环境噪声，位置放置比较灵活，既可以放 AEC 后，也可以放在ASR前面

一、子带分解（DFT fliterbank） STFT 短时傅里叶变换

信号的分频带处理，是语音信号处理中常用的手段
首先回顾DFT 公式，他将离散的时域（周期）信号，转换到频域

$\begin{aligned} X(k) &=\sum_{n=0}^{N-1} x(n) W_{N}^{n k} \\ X(k, l) &=\sum_{n=0}^{N-1} x(l+n) W_{N}^{n k} \end{aligned}$

k: frequency bin index （频率（点）序号）
l:frame index ( 帧移 frame shift 总大小)
n: time bin index (帧内，时间序号)
N:frame length
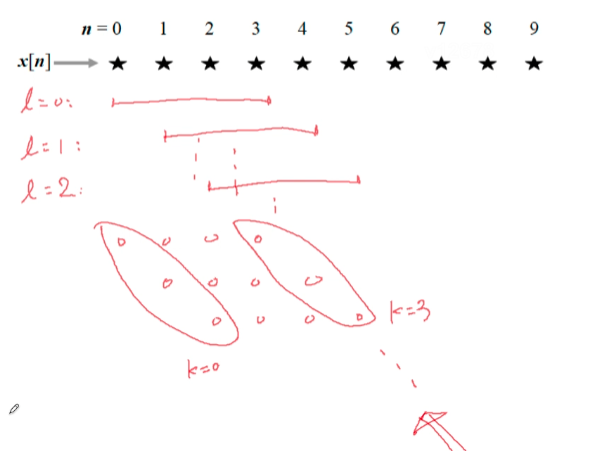
如图：以每次帧移为1举例（其实这样有很大的overlap）

红圈部分可以视为一个子(频)带。

选取合适的帧移因子(也可以叫抽取因子，因为这是每隔M个点抽取) $M$ ,则有

$\begin{aligned} X(k,l)=\sum_{n=0}^{N-1} x(l M+n) W_{N}^{n k} \end{aligned}$

1.1、DFT子带分解版本一（NS常用）

除此之外，再进行DFT之前还要加窗函数，这一点的必要性已经在博客的第二章（频谱泄露）讲过。

$\begin{aligned} X(k,l)=\sum_{n=0}^{N-1} x(l M+n) w(n)W_{N}^{n k} \end{aligned}$

我们把得到的$X(k,l)$ 叫做$ l$ 帧，子带$k$ 处的频谱
PS：更换窗函数并非抑制频谱泄露的唯一途径，还有就是增加窗函数的长度。举一个极端的例子，当窗函数无限长时，就意味着原始信号没有被截断，不截断就不会导致频谱泄露的发生。

1.2、DFT 子带分解版本二（AEC常用）

考虑使用更长的窗函数，例如$L=3N$
将会得到如下结果：

$\begin{aligned} X(k,l)=\sum_{n=0}^{L-1} x(l M+n) w(n)W_{N}^{n k} \end{aligned}$

特别注意，这里虽然和原来的式子只有求和符号区间的区别，但是，更改了这个区间之后，就不再是一个标准DFT了！！！因为 $W$因子的下标依旧是$N$.

那么如何计算这个非标准的DFT呢？
下面是流程图

graph TD
A[加L长的窗函数到目前处理的信号块] --> B(把这个L长的块分成数个N长的子块 不够就补零)
    B --> C[将子块对应点分别相加 得到 一个 N长块]
    C --> D[对该N长块进行N点DFT/FFT]
    D --> E[将L长的窗继续向前滑动M点]
    E --> A

二、噪声抑制 NS (Noise Suppression)

常见噪声场景及其分类

CAF（咖啡厅） Babble Noise
STR（街道） Street Noise
BUS（公交） Bus Noise
PED（）

噪声抑制方法的分类

从输入通道数来分
- 单通道噪声
- 多通道噪声
从噪声统计特征
- 平稳噪声
- 非平稳噪声（突发噪声，如：关车门、拍桌子）
降噪方案
- 被动降噪
- 主动降噪

这篇文章内容目前先研究单通道噪声、平稳噪声、被动降噪方案

评价指标：

信号层面
- Signal-to-noise ratio（SNR）
- Signal-to-distortion ratio（SDR）
- Mean opinion score（MOS）
- Perceptual evaluation of speech quality（PESQ）
- Short-time objective intelligibility（STOI）
语音识别率
- Word error rate（WER）

2.1、降噪算法基本框架：噪声估计& 增益因子估计

首先对于大部分降噪方法，都要经历两个步骤。

对噪声的估计（Noise estimation 、noise tracking）（也是噪声抑制的核心）
- 对噪声的一些统计特性特性进行估计
- 如：噪声的谱什么样？在那些频段、那些帧上存在噪声谱？
- 传统噪声估计的方法有：
  - 递归平均 Recursive Averaging
  - 最小值追踪 Minima controlled
  - 直方图估计 histogram
对增益因子的估计
- 谱减法
- 维纳滤波
- MMSE
- ……

2.2、噪声估计：以 MCRA 模型为例

Minima Controlled Recursive Averaging (MCRA) 最小追踪递归平均

传统噪声估计的方法(步骤) 有：

递归平均 Recursive Averaging
- 如果再某些频带内/帧内声音分量很低，或者存在的概率很低，那么就认为这是一个（纯）噪声的频带/帧，利用这些帧来估计其他频带/帧的噪声特性；反之，就不会选择那些声音分量小的频带/帧来估计噪声
最小值追踪 Minima controlled
- 由于语音信号的稀疏特性，即使语音存在，在一个短时窗内（0，5~1.5s），每个频带的最小值也会概率趋近于噪声功率。因此可以通过在短时窗内追踪最小值的方法获得每个频带的噪声估计。
直方图估计 histogram
-带噪语音信号的每个频带在一个短时窗内做直方图统计，出现频次最高的值对应这个频带的噪声水平。

2.2.1、MCRA 模型

MCRA就是前两者( Recursive Averaging\Minima controlled)的结合

graph TD
A[Minima controlled:利用局部最小值判断语音存在概率] --> B(语音存在概率)
    B --> C[recursive averaging:利用哪些频带进行噪声估计]

考虑一个加性噪声的模型

$y(n)=x(n)+d(n)$

输入信号经过overlap 分帧、加窗、傅里叶变换，也即信号的STFT表示：(DFT 子带分解版本一)

$\begin{aligned} Y(k,l)=\sum_{n=0}^{N-1} y(l M+n) h(n) e^{-j\frac{2\pi}{N}nk} \end{aligned}$

其中：
k: frequency bin index
l: time frame index
h: analysis window of size N (frame length)
M: frame shift

给定两个假设

$H_0(k,\mathcal{l})$:当前帧（帧号l）、频段(频点编号k) 语音不存在
$H_1(k,ℓ)$:当前帧（帧号l）、频段(频点编号k) 语音存在

那么再两个假设分别成立时有：

$\begin{aligned} &H_{0}(k, \ell): Y(k, \ell)=D(k, \ell) \\ &H_{1}(k, \ell): Y(k, \ell)=X(k, \ell)+D(k, \ell) \end{aligned}$

其中$X(k, \ell)$,$D(k, \ell)$分别表示纯净语音信号、噪声信号的STFT表示，
PS：作为（背景）噪声估计，估计的其实其实就是噪声的能量，也就是方差。因为我们把噪声视为一个零均值的高斯变量，所以只有方差这一个参数。

2.2.2、噪声估计算法

噪声估计递归方程

定义下面一个变量：
$\lambda_d(k,\ell)=E\left [\left | D(k,\ell)\right |^2\right])$,其物理含义是为$k$帧，$\ell$子带处的噪声方差（能量），也叫噪声谱。

想法是，用当前的噪声谱来“平滑地、递归的”估计下一帧当前频点的噪声谱。

$\begin{aligned} &H_{0}^{\prime}(k, \ell): \hat{\lambda}_{d}(k, \ell+1)=\alpha_{d} \hat{\lambda}_{d}(k, \ell)+\left(1-\alpha_{d}\right)|Y(k, \ell)|^{2} \\ &H_{1}^{\prime}(k, \ell): \hat{\lambda}_{d}(k, \ell+1)=\hat{\lambda}_{d}(k, \ell) \end{aligned}$

第一行意思是，如果假设当前帧子带存在语音，那么用当前帧子带的噪声谱与信号谱加权平均，来当作下一时刻的噪声谱的估计。$\alpha_{d}$ 是平滑因子
第二行意思是，如果假设当前帧子带不存在语音，那么直接用当前帧子带的噪声谱来当作对下一时刻的噪声谱的估计。

那么“语音存在与否”，这个信息相当的关键，我们定义语音存在的条件概率为

$p^{\prime}(k, \ell) \triangleq P\left(H_{1}^{\prime}(k, \ell) \mid Y(k, \ell)\right)$

那么对于噪声估计的递归方程改写为：（把两种假设融合在了一起）

$\begin{aligned} \hat{\lambda}_{d}(k, \ell+1)&=\hat{\lambda}_{d}(k, \ell) p^{\prime}(k, \ell) +\left[\alpha_{d} \hat{\lambda}_{d}(k, \ell)+\left(1-\alpha_{d}\right)|Y(k, \ell)|^{2}\right]\left(1-p^{\prime}(k, \ell)\right) \\ &=\tilde{\alpha}_{d}(k, \ell) \hat{\lambda}_{d}(k, \ell)+\left[1-\tilde{\alpha}_{d}(k, \ell)\right]|Y(k, \ell)|^{2} \\ \\ \tilde{\alpha}_{d}(k, \ell) &\triangleq \alpha_{d}+\left(1-\alpha_{d}\right) p^{\prime}(k, \ell) \end{aligned}$

所以问题的关键落在了：如何求取语音存在的概率$p^{\prime}(k, \ell)$？

语音存在（条件）概率

这里采用认为语音存在概率与 当前带噪语音的能量谱（也叫局部能量 local energy) $S(k,\ell)$ 和 指定长度窗内带噪语音的能量谱最小值 $S_{min}(k,\ell)$ 的比值有关。

求 $S(k,\ell)$

注意，这里的能量谱是经过频域和时间域的平滑操作得到的能量谱。

频域平滑，

$S_{f}(k, \ell)=\sum_{i=-w}^{w} b(i)|Y(k-i, \ell)|^{2}$

$b(i)$是频域窗，一般取窗函数参数 $w$ 为 1 或者 2 ,物理意义上就是对能量谱进行小范围内的加权平均。

时域平滑

$S(k, \ell)=\alpha_{s} S(k, \ell-1)+\left(1-\alpha_{s}\right) S_{f}(k, \ell)$

$\alpha_{s}$是是local ernergy 的时域 平滑因子

求 $S_{min}(k,\ell)$

采用局部最小值追踪的方案，设定一个时间窗$L$，作为参考,搜索局部最小值。

初始化

$\begin{aligned} S_{\min }(k, \ell) &=S(k, 0)\\ S_{t m p}(k, \ell) &=S(k, 0) \end{aligned}$

逐帧比较 （ $\ell $ 递增）

$\begin{aligned} S_{\min }(k, \ell) &=\min \left\{S_{\min }(k, \ell-1), S(k, \ell)\right\} \\ S_{t m p}(k, \ell) &=\min \left\{S_{t m p}(k, \ell-1), S(k, \ell)\right\} \end{aligned}$

当比较了L帧 $(\bmod (\ell, \mathrm{L})=0)$ 后

$\begin{aligned} &S_{\min }(k, \ell)=\min \left\{S_{t m p}(k, \ell-1), S(k, \ell)\right\} \\ &S_{t m p}(k, \ell)=S(k, \ell) \end{aligned}$

搜索窗的长度L会影响到噪声的跟踪速度，一般按照经验选0.5s~1.5s左右。

求$p^{\prime}(k, \ell)$

定义:

$\quad S_{r}(k, \ell) \triangleq \frac{S(k, \ell)}{S_{\min }(k, \ell)}$

则语音是否存在的判决式为:

$S_r(k,\ell)\overset{H_{1}^{\prime}}{ \underset{H_{0}^{\prime}}{\gtrless} } \delta$

根据上式，可以得到语音存在概率的迭代估计:

$\begin{aligned} \hat{p^{\prime}}(k, \ell)&=\alpha_{p} \hat{p}^{\prime}(k, \ell-1)+\left(1-\alpha_{p}\right) I(k, \ell) \\ I(k, \ell)&=\left\{\begin{matrix} 0 & S_{r}(k, \ell)> \delta\\ 1 & otherwise \end{matrix}\right. \end{aligned}$

其中$\delta $为，预定的门限 $\alpha_{p}\left(0<\alpha_{p}<1\right)$ 是语音存在概率的平滑因子。

总结：MCRA 噪声估计流程

流程	需要的公式
最小值跟踪法获得带噪语音的最小值，即噪声的初步估计	$S_{min}(k,\ell)$
根据噪声的初步估计，计算语音存在概率	$\hat{p^{\prime}}(k, \ell)=\alpha_{p} \hat{p}^{\prime}(k, \ell-1)+\left(1-\alpha_{p}\right) I(k, \ell) $
根据语音存在概率，计算噪声估计的平滑因子	$ \tilde{\alpha}_{d}(k, \ell) \triangleq \alpha_{d}+\left(1-\alpha_{d}\right) p^{\prime}(k, \ell) $
用递归平均法得到噪声估计	$ \hat{\lambda}_{d}(k, \ell+1)=\tilde{\alpha}_{d}(k, \ell) \hat{\lambda}_{d}(k, \ell)+[1-\tilde{\alpha}_{d}(k, \ell)]	Y(k, \ell)	^{2}$

MCRA 参数参考表

$\begin{aligned} &N=512(32 m s) \\ &M=128(75 \% \text { overlap }) \\ &\alpha_{d}=0.95 \\ &w=1 \\ &\alpha_{s}=0.8 \\ &L=125(1 \text { s minima search window }) \\ &\delta=5 \\ &\alpha_{p}=0.2 \end{aligned}$

2.3、增益因子的确定

Q:当噪声估计已知以后，如何进行噪声抑制？
A:”增益因子”与“带噪语音相乘”即可

$\hat{X}(k,\ell)=G(k,\ell)Y(k,\ell)$

或者写成 $G(k,\ell)Y$ ，在传统的语音降噪领域，我们将其称为”增益因子”，在基于深度学习的领域普遍称其为 “Mask估计”，Ideal Mask/Ratio MasK ，后者与传统的降噪等价

$|\hat{X}(k,\ell)|^2=G^2(k,\ell)Y^2(k,\ell)$

确定增益因子的方法：

谱减法
维纳滤波
MMSE
……

2.3.1、谱减法：求增益因子

基本假设：噪声是平稳的，缓慢变化的

思想：将把接收信号中的噪声谱减去即可

根据等式：

$|\hat{X}(k)|^{2}=G^{2}(k)|Y(k)|^{2}$

得到增益因子的表达式:

$\begin{aligned} G(k)=\sqrt{\frac{|\hat{X}(k)|^{2}}{|Y(k)|^{2}}} &=\sqrt{\frac{|Y(k)|^{2}-|\widehat{D}(k)|^{2}}{|Y(k)|^{2}}}=\sqrt{\frac{|Y(k)|^{2}-\lambda_{d}(k)}{|Y(k)|^{2}}} \\ &=\sqrt{1-\frac{\lambda_{d}(k)}{|Y(k)|^{2}}}=\sqrt{1-\frac{1}{\gamma(k)}} \end{aligned}$

其中$\begin{aligned} \gamma(k)=\frac{|Y(k)|^{2}}{\lambda_d(k)}\end{aligned}$ 称为后验信噪比。（但是请注意，这并非严格意义上的信噪比，因为信噪比的定义是信号能量比上噪声能量，而这个式子只有分母满足要求是噪声能量，但是分子确实接受信号的能量，也即信号能量加上噪声能量。）

所以总结来说，谱减法的增益因子由所谓的后验信噪比决定。

2.3.2、维纳滤波（频域）求增益因子

思想：估计出的纯净语音幅度谱与真实幅度谱的均方误差最小

频域估计误差 :

$E(k)=X(k)-\hat{X}(k)=X(k)-G(k) Y(k)$

目标函数 :

$J=E\left[|E(k)|^{2}\right]$

其实和时域的维纳滤波没什么不同，本质上都是使得目标函数（参考信号与输出信号的差）最小化。时序得到是系统（滤波器）系数，频域得到的就是“增益因子”

最小化目标函数，可以得到频域维纳滤波器的增益因子 :

$G(k)=\frac{\lambda_{x}(k)}{\lambda_{x}(k)+\lambda_{d}(k)}=\frac{\xi(k)}{\xi(k)+1}$

这一步
这里有一个推导，但一些步骤不是很懂

$\begin{aligned} \lambda_x(k)&=E\left[\left|X(k) \right|^2 \right]\\ \xi(k)&=\frac{\lambda_x(k)}{\lambda_{d}(k)} \end{aligned}$

$\xi(k)$称为先验信噪比，直观上，先验信噪比更符合信噪比的定义，似乎也更精确，但是缺点就是，先验信噪比不好算。因为原始纯净信号不知道啊

先验信噪比 & 后验信噪比

先验信噪比：

$\xi(k)=\frac{\lambda_x(k)}{\lambda_{d}(k)}$

后验信噪比：

$\begin{aligned} \gamma(k)=\frac{|Y(k)|^{2}}{\lambda_d(k)}\end{aligned}$

根据后验信噪比估计先验信噪比 ：判决引导法（Decision Direct）

$\xi(k, l)=\alpha_{D D} \frac{|\hat{X}(k, l-1)|^{2}}{\lambda_{d}(k, l-1)}+\left(1-\alpha_{D D}\right) \max \{\gamma(k, l)-1,0\}$

有时第一项的分母也可以用$\lambda_{d}(k, l)$
$\alpha_{D D}$ 的经验值为：0.95-0.98

总结一下，

在谱减法当中采用后验信噪比来算增益因子
在维纳滤波当中采用先验信噪比来算增益因子

2.3.3、 MMSE 求增益因子

$\begin{aligned} &G(k)=\Gamma(1.5) \frac{\sqrt{v(k)}}{\gamma(k)} \exp \left(-\frac{v(k)}{2}\right)\left[(1+v(k)) I_{0}\left(\frac{v(k)}{2}\right)+v(k) I_{1}\left(\frac{v(k)}{2}\right)\right] \\ &v(k)=\frac{\xi(k)}{1+\xi(k)} \gamma(k) \end{aligned}$

可以看到，他同时用到了先验信噪比和后验信噪比

论文：Speech Enhancement Using a Minimum Mean-square Error Short-Time Spectral Amplitude Estimator. Ephraim & Malah, 1984”

总结

目前为止，已经讲了完了单通道平稳噪声的两大降噪步骤，噪声估计和增益因子的确定，其中，噪声估计的估计质量直接影响后续增益因子从而影响降噪质量。
另外，对于三种增益因子的确定方案：谱减法其实效果不是特别好，容易产生音乐噪声；维纳滤波和 MMSE 的估计方案用的更多一些。

语音信号处理（四）噪声抑制

一、子带分解（DFT fliterbank） STFT 短时傅里叶变换

1.1、DFT子带分解版本一（NS常用）

1.2、DFT 子带分解版本二（AEC常用）

二、噪声抑制 NS (Noise Suppression)

2.1、降噪算法基本框架：噪声估计& 增益因子估计