语音信号处理（六） 阵列信号处理

一、阵列信号处理的基本概念

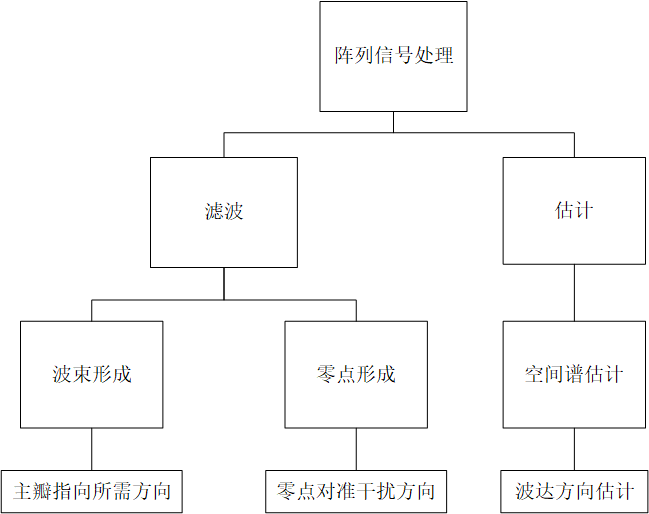
阵列信号处理大致可以分为两种用途：一个是滤波一个是估计。这两个用途其实在单通道的信号处理也有相似的概念，只不过这种滤波和估计被拓展到空间域之上。

1.1、阵列信号模型

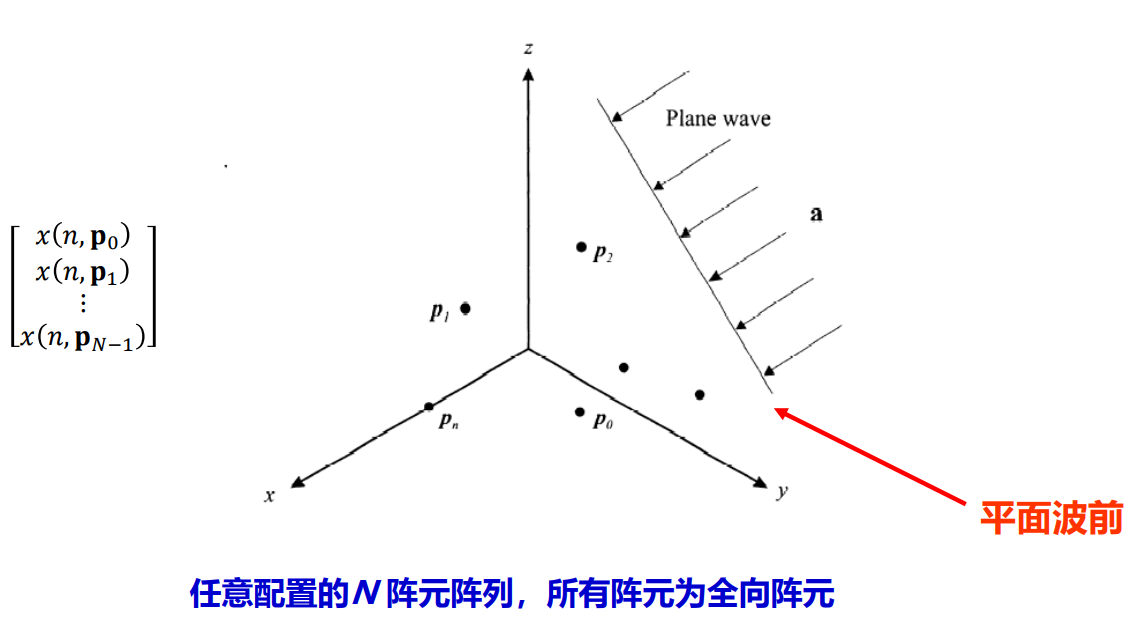
考虑一个三维立体模型，里面有n个任意位置摆放的阵元，且阵元都是全向阵元。声源从a方向入射。

如图所示，模型可以提取两种信息：

• 1、N个权阵元的摆放位置
• 2、声源入射方向
  在这样两层信息的加持下，就可以写阵列输入信号的表达形式： $$\begin{gathered} \mathbf{x}(n, \mathbf{p})=\left[\begin{array}{c} x\left(n, \mathbf{p}_{0}\right) \\ x\left(n, \mathbf{p}_{1}\right) \\ \vdots \\ x\left(n, \mathbf{p}_{N-1}\right) \end{array}\right] \end{gathered}$$

这个接受信号的矩阵其实也包含着两层信息：

• 由于每一个阵元接受的其实是同一个声源发出的信息，所以每一路信号包含着x(n)信号，也即是同源的
• 由于每一个阵元位置的不同，就会收到每一个阵元空间方位（空间坐标）$\mathbf{p}_i$的影响。

阵列接收信号（时域）的矩阵表示：

$$y(n)=\sum_{m=-\infty}^{\infty} \mathbf{h}^{T}(n-m) \mathbf{x}(m, \mathbf{p})$$

阵列信号的频域表示

$$Y(\omega)=\mathbf{H}^{T}(\omega) \mathbf{X}(\omega)$$

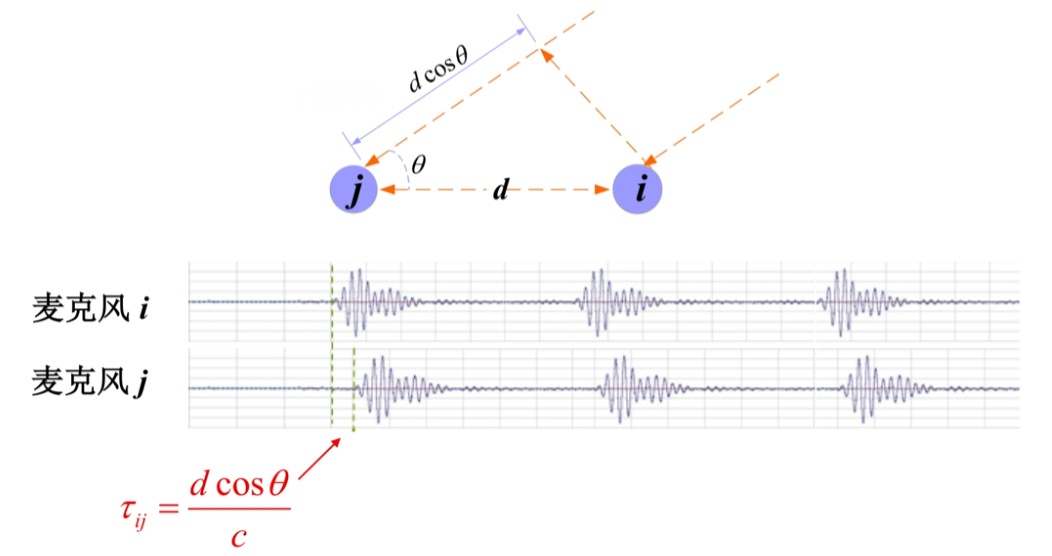
考虑声音的平面波入射的情况（绝大部分情况下的阵元模型都满足这一假设），在这种情况下，阵元信号的差异就主要体现在时延上，时延由阵元坐标决定 ：

$$\mathbf{x}(n, \mathbf{p})=\left[\begin{array}{c} x\left(n-\tau_{0}\right) \\ x\left(n-\tau_{1}\right) \\ \vdots \\ x\left(n-\tau_{N-1}\right) \end{array}\right]$$

另外还需要一个对比的阵元:每一个阵元他与哪一个阵元相比他的时延为$\tau_i$?
假设有一个阵元位于坐标原点（其实可以没有这样一个阵元，只是假设有），其他，其他阵元的时延可以由下式决定

$$\begin{aligned} \tau_{i} &=\frac{\mathbf{a}^{T} \mathbf{p}_{i}}{c}, \quad i=0, \ldots, N-1 \\ \end{aligned}$$

其中$\boldsymbol{a}$为声源入射方向，$\theta$为声源入射方向与$z$轴的夹角，也叫俯仰角，$\phi$角为入射射线投影到x-y平面后于x轴正方向的夹角，也叫方位角。注意 入射方向 每个坐标前面都带有负号！

$$\begin{aligned} \boldsymbol{a} &=\left[\begin{array}{c} -\sin \theta \cos \phi \\ -\sin \theta \sin \phi \\ -\cos \theta \end{array}\right] \end{aligned}$$

这样，原来的接收信号的频域表示就可以写为（因为时域的演示对应为频域的相移）

$$\mathbf{X}(\omega)=\left[\begin{array}{c} e^{-j \omega \tau_{0}} \cdot X(\omega) \\ e^{-j \omega \tau_{1}} \cdot X(\omega) \\ \vdots \\ e^{-j \omega \tau_{N-1}} \cdot X(\omega) \end{array}\right]=\left[\begin{array}{c} e^{-j \omega \tau_{0}} \\ e^{-j \omega \tau_{1}} \\ \vdots \\ e^{-j \omega \tau_{N-1}} \end{array}\right] X(\omega)$$

部分文献将 乘式左边的列向量 称为 方向向量
将时延公式带入上式，那么输入信号的频域表示也可以写成：

$$\omega \tau_{i}=\omega \frac{\mathbf{a}^{T} \mathbf{p}_{i}}{c}=\left(\frac{\omega}{c} \mathbf{a}\right)^{T} \mathbf{p}_{i}=\mathbf{k}^{T} \mathbf{p}_{i}$$ $$\mathbf{X}(\omega)=\left[\begin{array}{c} e^{-j \mathbf{k}^{T} \mathbf{p}_{0}} \\ e^{-j \mathbf{k}^{T} \mathbf{p}_{1}} \\ \vdots \\ e^{-j \mathbf{k}^{T} \mathbf{p}_{N-1}} \end{array}\right] X(\omega)=\mathbf{v}_{\mathbf{k}}(\mathbf{k}) X(\omega)$$

其中$\mathbf{k}$也被称为波数向量，之所以这样叫，因为$\begin{aligned} \mathbf{k}= \frac{\omega}{c} \mathbf{a}=\frac{2\pi f}{c} \mathbf{a}= \frac{2\pi }{\lambda} \mathbf{a} \end{aligned}$,那么方向向量的相位就可以写为波数向量于方向向量的向量乘积。 这种写法得到的方向向量也叫“阵列流行矢量”，注意它其实和方向向量是一个东东。 从这阵列流形矢量的定义来看，他已经规定好了一个阵列模型的所有空间信息了：1、各个阵元的空间方位，2、声源到达方向
其中，这个$\frac{2\pi }{\lambda}$ 我们在大学物理下或者电磁场理论中见过，叫做波数.

频率$\omega$的单位是rad/s，表示时间变化一秒，相位的变化量，描述波动随时间的变化，称为时间角频率;波数k的单位是rad/m，表示空间距离变化一米，相位的变化量，描述波动随空间的变化，称为空间角频率。

转自：知乎

二、波束成形

2.1、波束形成的概念

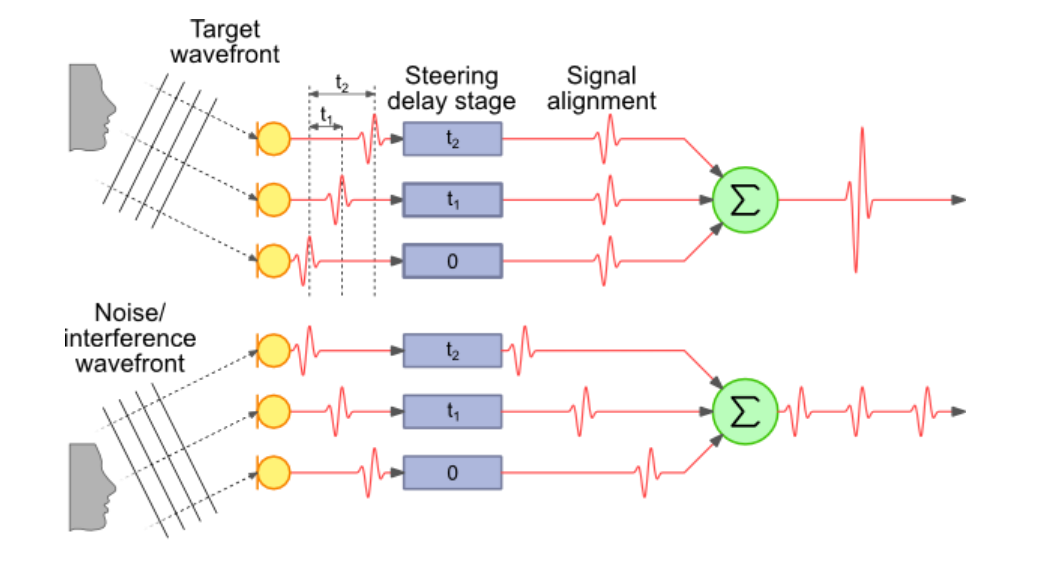
所谓波束成形就是 通过多 天线阵列相关性 特定方向的音源获得增益 ，而干扰方向没有改进或者增益为零（如图中上半部分 有三倍的增益，下面只有一杯增益 而且还被分散了），
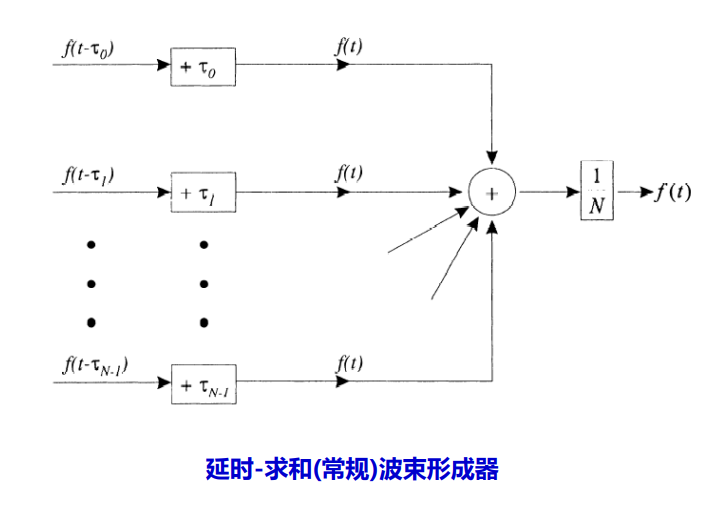
如图这种形式叫做延迟求和波束形成，是一种最基本最简单的波束形成方式。将时延模块改成滤波器模块，将变成更为通用的 滤波求和波束形成。所谓研究波束形成就是研究这个滤波器是怎样设计的。

假设已经得到了阵列输入信号信号模型，将每一路输入信号加入一个时延，使得每一路信号在时间上“对齐”：

$$h_i(n)=\frac{1}{N}\delta(n+\tau_i)$$

则

$$y(n)=x(n)$$

这种处理方式称为延迟求和波束形成（delay-and-sum beamformer / conventional beamformer）；这种方案虽然不是最优的波数形成方案，但是好在稳定，现在一般的系统还可以见到这种形式的实现。

一个重要的问题是，我们需要一个描述阵列系统对于任意输入信号的响应函数：

$$Y(\omega)=\mathbf{H}^T(\omega)\mathbf{X}(\omega)=\mathbf{H}^T(\omega)\mathbf{v_k(k)}X(\omega)$$

频率波数响应（frequency-wavenumber response

$$\Upsilon(\omega, \mathbf{k})=\mathbf{H}^{T}(\omega) \mathbf{v}_{\mathbf{k}}(\mathbf{k})$$

波束方向图( beam pattern )
即频率-波数响应在球面 $k=2 \pi / \lambda$ 上的取值 :

$$B(\omega: \theta, \phi)=\left.\Upsilon(\omega, \mathbf{k})\right|_{\mathbf{k}=\frac{2 \pi}{\lambda} \mathbf{a}}$$

对于波束方向图，如果给定频 率 $\omega_{c}$ ，频率-波数响应可以简化为：

$$\Upsilon(\omega, \mathbf{k})=\mathbf{H}^{T}\left(\omega_{c}\right) \mathbf{v}_{\mathbf{k}}(\mathbf{k})=\mathbf{w}^{H} \mathbf{v}_{\mathbf{k}}(\mathbf{k})=\left[\begin{array}{llll} w_{0}^{*} & w_{1}^{*} & \ldots & w_{N-1}^{*} \end{array}\right] \mathbf{v}_{\mathbf{k}}(\mathbf{k})$$

2.2、举例，以均匀线性阵列（ULA）为例

Uniform Linear Array

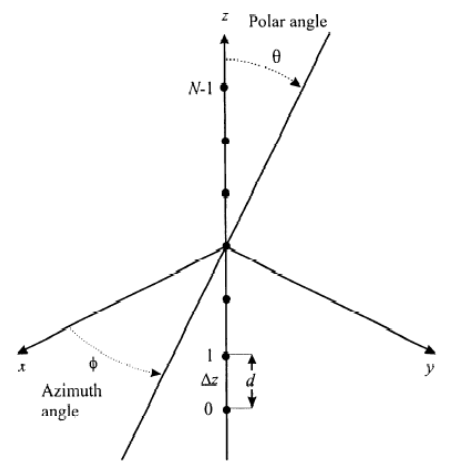
假设阵列的排列方向位于$z$轴之上，如图；

记为每个阵元的坐标为

$$p_{z_i}=(i-\frac{N-1}{2})d,i=0,1,……,N-1\\ p_{x_i}=p_{y_i}=0$$

$d$为阵元之间的距离。那么现在已经得到了阵列各个阵元的三维坐标向量了，将他带入阵列流形矢量当中，可以得到

$$\mathbf{v}_{\mathbf{k}}(k_z)=[e^{-j(0-\frac{N-1}{2})k_z d}, e^{-j(1-\frac{N-1}{2})k_z d},……,e^{-j(N-1-\frac{N-1}{2})k_z d} ] ^T \\ k_z=-\frac{2\pi}{\lambda}\cos(\theta)$$

显然，ULA的频率-波数响应可以表示为：

$$\Upsilon\left(\omega, k_{z}\right)=\mathbf{w}^{H} \mathbf{v}_{\mathbf{k}}\left(k_{z}\right)=\sum_{i=0}^{N-1} w_{i}^{*} e^{-j\left(i-\frac{N-1}{2}\right) k_{z} d}$$

相应的beam pattern可以表示为：

$$B_{\theta}(\theta)=\mathbf{w}^{H} \mathbf{v}_{\theta}(\theta)=e^{-j\left(\frac{N-1}{2}\right) \frac{2 \pi d}{\lambda} \cos \theta} \sum_{i=0}^{N-1} w_{i}^{*} e^{j i \frac{2 \pi d}{\lambda} \cos \theta}, \quad 0 \leq \theta \leq \pi$$

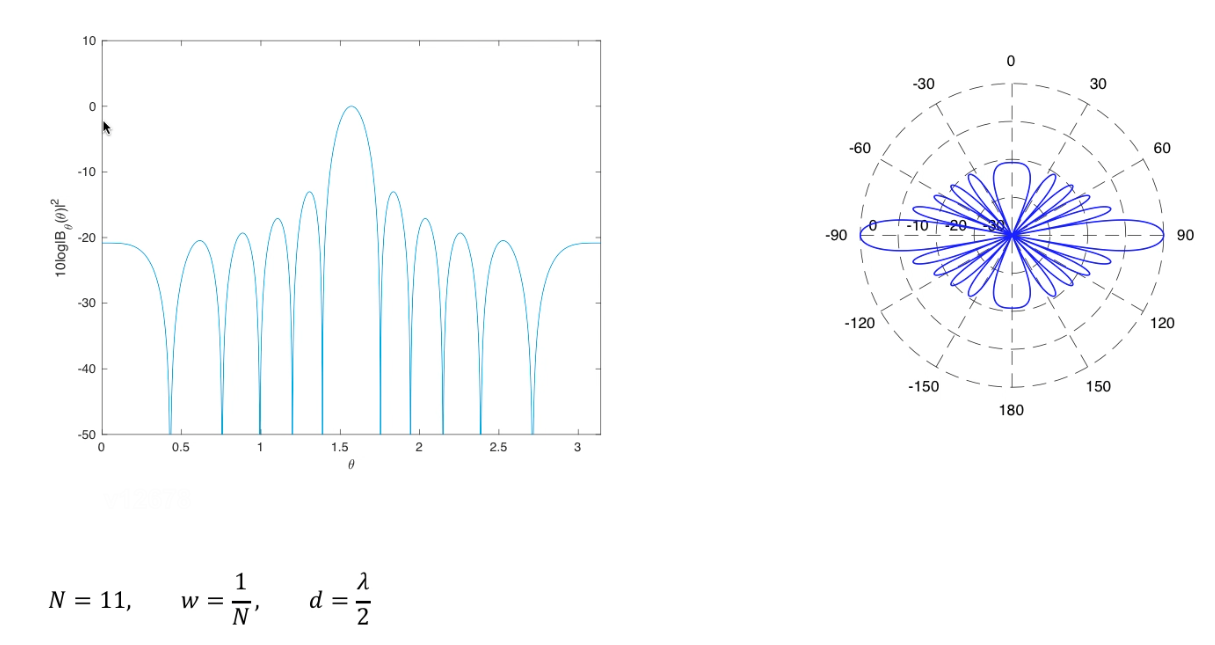
显然，该阵列的波数方向图只由俯仰角 $\theta$ 决定。

这个式也可以写成以下三种等价形式：

$$\begin{aligned} &B_{\theta}(\theta)=\mathbf{w}^{H} \mathbf{v}_{\theta}(\theta)=e^{-j\left(\frac{N-1}{2}\right) \frac{2 \pi d}{\lambda} \cos \theta} \sum_{i=0}^{N-1} w_{i}^{*} e^{j i \frac{2 \pi d}{\lambda} \cos \theta}, \quad 0 \leq \theta \leq \pi\\ & let \quad u=\cos \theta\\ &B_{u}(u)=\mathbf{w}^{H} \mathbf{v}_{u}(u)=e^{-j\left(\frac{N-1}{2}\right) \frac{2 \pi d}{\lambda} u} \sum_{i=0}^{N-1} w_{i}^{*} e^{j i \frac{2 \pi d}{\lambda} u}, \quad-1 \leq u \leq 1\\ & let \quad \psi=\frac{2 \pi d}{\lambda} u\\ &B_{\psi}(\psi)=\mathbf{w}^{H} \mathbf{v}_{\psi}(\psi)=e^{-j\left(\frac{N-1}{2}\right) \psi} \sum_{i=0}^{N-1} w_{i}^{*} e^{j i \psi}, \quad-\frac{2 \pi d}{\lambda} \leq \psi \leq \frac{2 \pi d}{\lambda} \end{aligned}$$

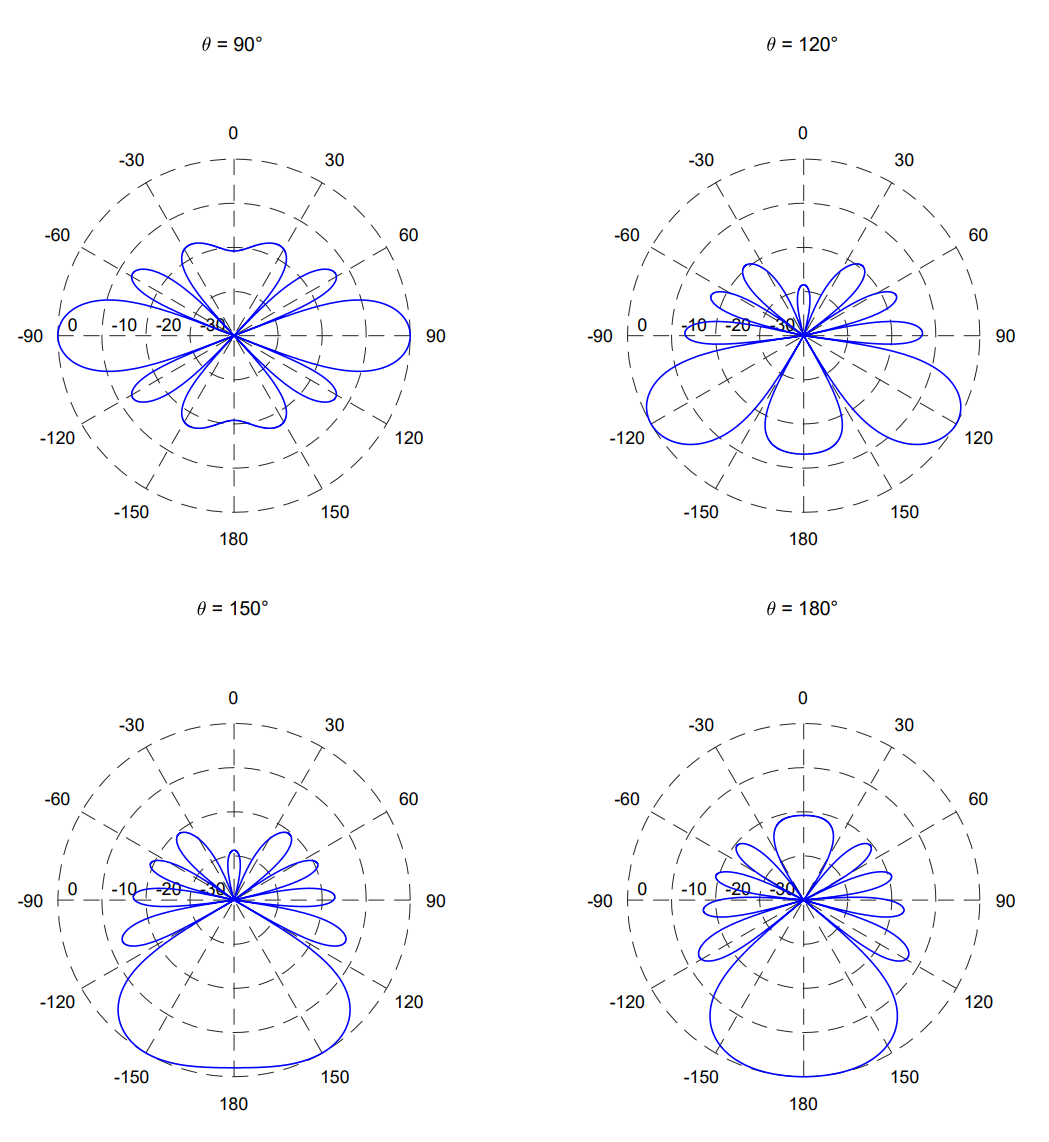
经计算可以得到这样的 波束方向图。可以明显看到，俯仰角为$90^o$时（左边对应 $\pi/2$）阵列增益最大，这个方向也叫做主波束方向

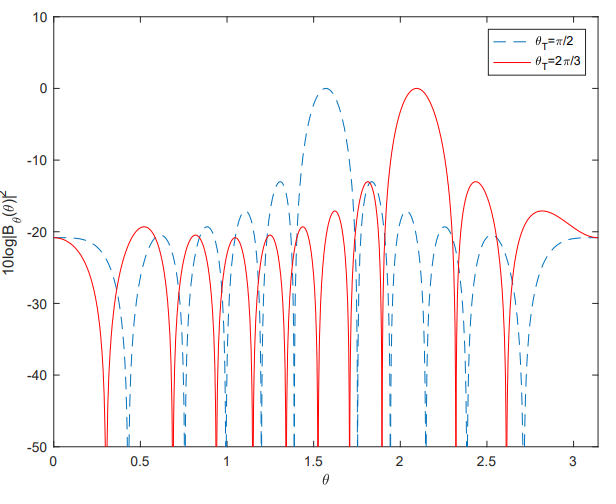
2.3、主波束调向(beam steering)

如果在实际项目当中需要改变主波束的方向时，就需要调整频率-波数响应函数。

$$\begin{gathered} \Upsilon\left(\omega, \mathbf{k}-\mathbf{k}_{T}\right) \leftarrow \Upsilon(\omega, \mathbf{k}) \end{gathered}$$

这样波数的指向就变成了$\mathbf{k}_{T}$对应的方向，这个”改写”的操作其实是作用在阵列流形矢量当中的。如下：

$$\begin{gathered} {\left[\begin{array}{c} e^{-j\left(\mathbf{k}-\mathbf{k}_{T}\right)^{T} \mathbf{p}_{0}} \\ e^{-j\left(\mathbf{k}-\mathbf{k}_{T}\right)^{T} \mathbf{p}_{1}} \\ \vdots \\ e^{-j\left(\mathbf{k}-\mathbf{k}_{T}\right)^{T} \mathbf{p}_{N-1}} \end{array}\right] \leftarrow\left[\begin{array}{c} e^{-j \mathbf{k}^{T} \mathbf{p}_{0}} \\ e^{-j \mathbf{k}^{T} \mathbf{p}_{1}} \\ \vdots \\ e^{-j \mathbf{k}^{T} \mathbf{p}_{N-1}} \end{array}\right]} \\ \end{gathered}$$

改写之后对于对于整个系统的修正可以等价到系统的权值向量当中，就是将 下列的列向量点乘 原来的权值向量。

$$\begin{gathered} \mathbf{w}_{T} \leftarrow\left[\begin{array}{c} e^{j \mathbf{k}_{T}^{T} \mathbf{p}_{0}} \\ e^{j \mathbf{k}_{T}^{T} \mathbf{p}_{1}} \\ \vdots \\ e^{j \mathbf{k}_{T}^{T} \mathbf{p}_{N-1}} \end{array}\right] \odot \mathbf{w} \end{gathered}$$

对于上述调向 有一个重要的问题，
1、$\mathbf{k}_{T}$怎么求？

2.4、方向图合成

频率-波数响应与权重向量之间的傅里叶变换关系？

$$B_{\psi}(\psi)=\mathbf{w}^{H} \mathbf{v}_{\psi}(\psi)=e^{-j\left(\frac{N-1}{2}\right) \psi} \sum_{i=0}^{N-1} w_{i}^{*} e^{j i \psi}, \quad-\frac{2 \pi d}{\lambda} \leq \psi \leq \frac{2 \pi d}{\lambda}\\ =e^{-j\left(\frac{N-1}{2}\right) \psi} \left(\sum_{i=0}^{N-1} w_{i} e^{-j i \psi}\right)$$

所以，我们可以利用时频分析的方法，修正线性阵列波束方向图，尽量减小旁瓣，保持最小的主瓣展宽程度——谱加权方法。

加权函数多为实对称函数，为了表述方便，定义：

$$\begin{aligned} \tilde{\imath}=\left(i-\frac{N-1}{2}\right), \quad & i=0,1, \ldots, N-1 \\ \tilde{\imath} &=-\frac{N-1}{2}, \ldots, \frac{N-1}{2} \end{aligned}$$

可以利用fir滤波器中的一些窗函数对权值向量进行加权。但注意需要将主瓣的能量增益归一化到0dB才能更好的对比。

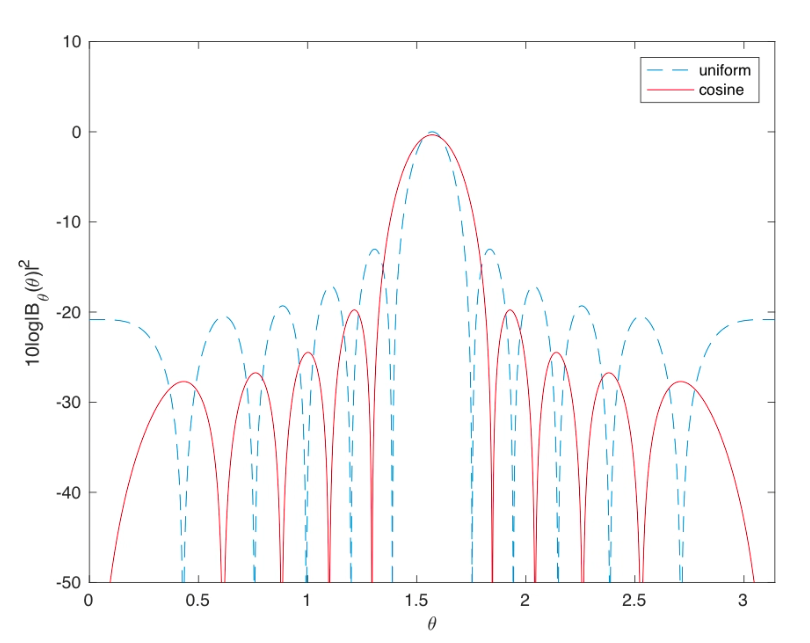
cosine 加权

$$w_{\tilde{\imath}}=\sin \left(\frac{\pi}{2N}\right)\cos\left(\pi \frac{\tilde{\imath}}{N}\right)$$

可以看到 经过加权之后，旁瓣有着明显的抑制，但是带来的代价就是主瓣 有了适当扩展

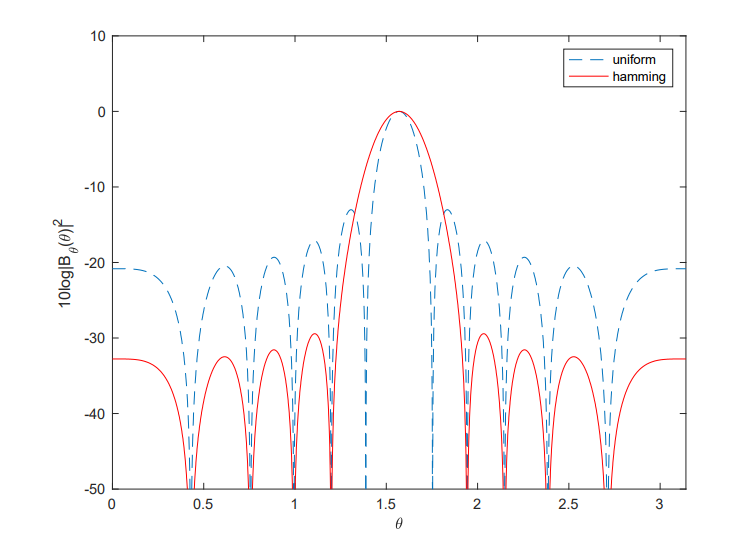
hamming 加权

2.5、零点调向（null steering / sidelobe canceller）

有时，我们希望阵列在某个或某些方向上的响应为零（或者响应尽可能小），这些方向称作零点
（null）方向。
目标：设计权值向量，满足特定的约束条件：

$$\begin{aligned} &\left\{\begin{array}{c} \mathbf{w}^{H} \mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{T}\right)=1 (无畸变响应约束)\\ \mathbf{w}^{H} \mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{i}\right)=0,(零点约束) \end{array} \quad i=1,2, \ldots, M_{0}\right. \\ &\mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{i}\right)=\left[\begin{array}{c} e^{-j \mathbf{k}_{i}^{T}} \mathbf{p}_{0} \\ e^{-j \mathbf{k}_{i}^{T} \mathbf{p}_{1}} \\ \vdots \\ e^{-j \mathbf{k}_{i}^{T} \mathbf{p}_{N-1}} \end{array}\right] \end{aligned}$$

无畸变约束条件：对于$\mathbf{k_T}$方向入射来的信号能够无畸变的接收
零点约束条件:对于$\mathbf{k_i}$方向入射的信号希望能够尽可能地抑制或者消除

零点调向

目标：选择权值$𝐰$，满足零点约束条件，利用最小二乘原则，拟合一个理想方向图$𝐰_𝑑$。$𝐰_𝑑$一般用没有零点约束条件下的权值向量来代替。

把全部地$M_0$个零点约束条件，写成矩阵的形式————“零阶约束”

$$\mathbf{C}=\left[\mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{1}\right) ,\mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{2}\right) ,……,\mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{M_0}\right) \right ]$$

则可以利用拉格朗日法，解决优化问题：

$$\left\{\begin{array}{l} \min \varepsilon=\left\|\mathbf{w}_{d}-\mathbf{w}\right\|^{2} \\ \text { s.t. } \mathbf{w}^{H} \mathbf{C}=\mathbf{0} \end{array}\right.$$

求解步骤

目标函数:

$$\mathcal{L}=\left(\mathbf{w}_{d}-\mathbf{w}\right)^{H}\left(\mathbf{w}_{d}-\mathbf{w}\right)+\mathbf{w}^{H} \mathbf{C} \lambda+\lambda^{H} \mathbf{C}^{H} \mathbf{w},$$

对w求导得到:

$$-\mathbf{w}_{d}^{H}+\mathbf{w}^{H}+\lambda^{H} \mathbf{C}^{H}=\mathbf{0}$$

将约束条件 $\mathbf{w}^{H} \mathbf{C}=\mathbf{0}$ 代入(6.24)式，求出拉格朗日因子:

$$\lambda^{H}=\mathbf{w}_{d}^{H} \mathbf{C}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1}$$

求得最优权值:

$$\mathbf{w}^{H}=\mathbf{w}_{d}^{H}-\lambda^{H} \mathbf{C}^{H}=\mathbf{w}_{d}^{H}\left(\mathbf{I}_{N}-\mathbf{C}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1} \mathbf{C}^{H}\right)$$

结论：最优权值是从理想权值中减去一个由约束矢量的线性组合形成的一个分量

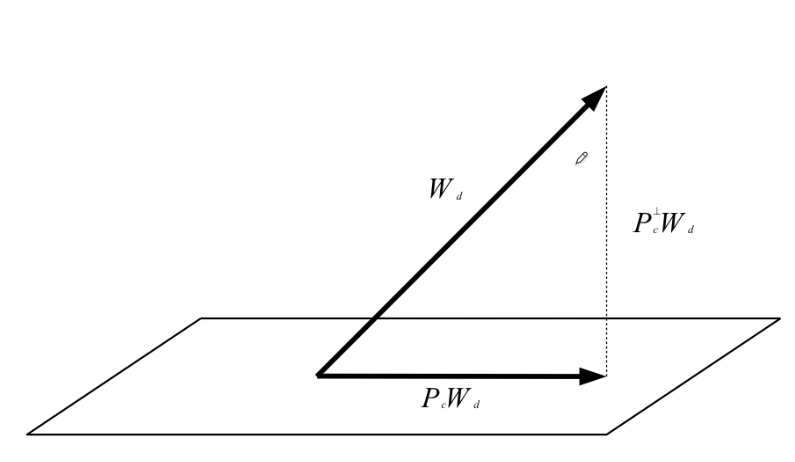
投影矩阵和正交投影矩阵 :

$$\begin{aligned} &\mathbf{P}_{\mathbf{C}}=\mathbf{C}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1} \mathbf{C}^{H} \\ &\mathbf{P}_{\mathbf{C}}^{\perp}=\mathbf{I}_{N}-\mathbf{C}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1} \mathbf{C}^{H} \end{aligned}$$

容易验证， $\mathbf{P}_{\mathbf{C}}$ 和 $\mathbf{P}_{\mathbf{C}}^{\perp}$ 既是 “幂等矩阵”，又是 “共轭对称矩阵”，所以它们都属于投影矩阵。且$\mathbf{P}_{\mathbf{C}}$ 与 $\mathbf{P}_{\mathbf{C}}^{\perp}$ 相互垂直。
因此 :

$$\mathbf{w}^{H}=\mathbf{w}_{d}^{H} \mathbf{P}_{\mathbf{C}}^{\perp}$$

举一个形象点的例子，如果我们已经有了理想的权值向量$\mathbf{W}_d$（他是没有零点约束情况下的向量），如果希望它能够满足一个约束条件，约束条件由平面$\mathbf{P}_{\mathbf{C}}$ 构成（可以理解为由约束矩阵C的各个列向量张成的线性空间），那么最优的 权值向量 $W$ 应该在这个平面上没有任何分量，也即应该垂直于该 约束平面。而垂直于该平面的向量为$\mathbf{P}_{\mathbf{C}}^{\perp}\mathbf{W}_d$,即为所求。

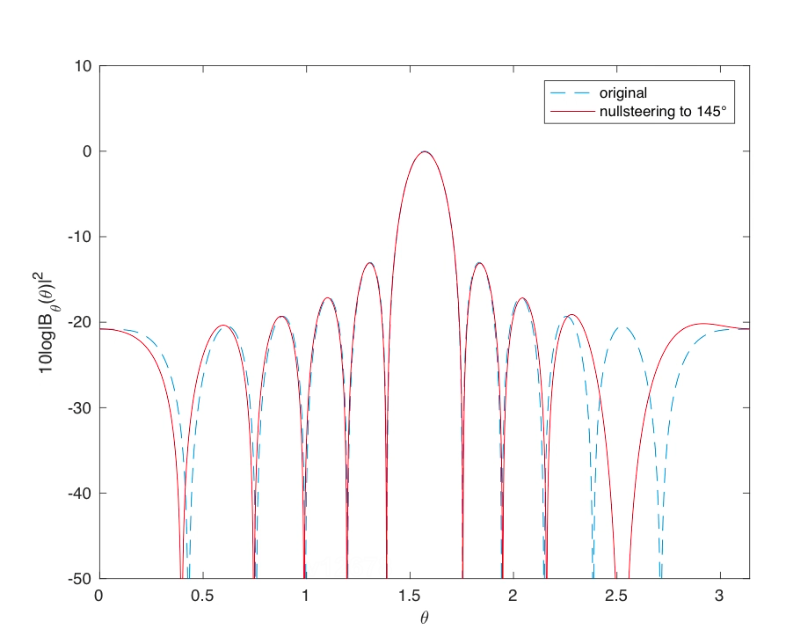
下图是对145°方向进行了一个零点约束的结果。

三、常见的波束形成方法

Delay-and-sum（DS）
Minimum Variance Distortionless Response（MVDR）
Linearly Constrained Minimum Variance（LCMV）
Generalized Sidelobe Canceller（GSC）

3.1、Delay-and-sum (DS) Beamformer

延迟求和波束形成方法
虽然延迟求和波束形成（常规波束形成）对于干扰的抑制作用，尤其是对方向性干扰的抑制效果并不是最好的，但是但他对于目标方向上接受的稳定性确实最高的。所以实际项目当中也有很多的应用场景，比如GSC方法的魔魁啊中就用到了 DS Beamformer

3.2、Minimum Variance Distortionless Response（MVDR）

最小方差无畸变响应 波束形成器

语音信号从已知方向𝐤𝑠入射，我们推导出最优波束形成器，提供对目标语音的最小方差无偏估计，得到无畸变波束形成器MVDR，或者Capon波束形成器。

考虑一个信号+ 噪声 的模型

$$\mathbf{X}(\omega)=\mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{s}\right) X(\omega)+\mathbf{N}(\omega)=\mathbf{X}_{s}(\omega)+\mathbf{N}(\omega)$$

目标：希望利用$\mathbf{X}(\omega)$得到关于$X(\omega)$的无偏、最小方差估计。
方案：在满足无畸变接收的前提下，寻找最优权值 $\mathbf{w}^{H}$ ，最小化输出功率（方差）

$$\begin{aligned} E|Y(\omega)|^{2}=E\left|\mathbf{w}^{H} \mathbf{X}(\omega)\right|^{2} &=\mathbf{w}^{H} E\left[\mathbf{X}(\omega) \mathbf{X}^{H}(\omega)\right] \mathbf{w} \\ &=\mathbf{w}^{H} \mathbf{R}_{\mathbf{x x}}(\omega) \mathbf{w} \end{aligned}$$

求解如下优化问题：

$$\left\{\begin{array}{l} \min \mathbf{w}^{H} \mathbf{R}_{\mathbf{x x}}(\omega) \mathbf{w} \\ \text { s.t. } \mathbf{w}^{H} \mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{s}\right)=1 \end{array}\right.$$

通过拉格朗日乘子法，得到最优解，也即capon最优解 :

$$\mathbf{w}_{c}=\frac{\mathbf{R}_{\mathbf{X X}}^{-1}(\omega) \mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{s}\right)}{\mathbf{v}_{\mathbf{k}}^{H}\left(\mathbf{k}_{s}\right) \mathbf{R}_{\mathbf{X X}}^{-1}(\omega) \mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{s}\right)}$$

可以看出，结果主要取决于两个变量，
第一个就是阵列流形矢量。也即必须要知道或者准确的估计到信号的入射方向。
第二个是信号的相关矩阵。

可以使用 $\mathbf{R}_{\mathbf{n n}}(\omega)$ 代替 $\mathbf{R}_{\mathrm{xx}}(\omega)$ :
可以这样理解，我们在求解的过程中，已经在语音信号的方向上施加了一个无畸变约束，这就相当于我们在语音信号保持不变的前提下使得总的输出方差最小。那么达成目标的手段就仅需将噪声最小化，所以很多时候可以将噪声的相关矩阵来代替接收信号的相关矩阵。

$$\mathbf{w}_{c}=\frac{\mathbf{R}_{\mathbf{n n}}^{-1}(\omega) \mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{s}\right)}{\mathbf{v}_{\mathbf{k}}^{H}\left(\mathbf{k}_{s}\right) \mathbf{R}_{\mathbf{n n}}^{-1}(\omega) \mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{s}\right)}$$

• MVDR是一种自适应波束形成器，而DS是固定波束形成器。
• 当各个通道的噪声互不相关，并且具有相同功率的时候，MVDR退化成DS。
• 如果噪声是一个点声源，MVDR会自适应地在噪声方向形成一个零点。
• MVDR的性能依赖于对阵列流形矢量𝐯𝐤 𝐤𝑠 和相关矩阵𝐑𝐧𝐧(𝜔) 的估计。
• 对MVDR的约束条件进行扩展，可以得到LCMV

3.3、Linearly Constrained Minimum Variance (LCMV)

线性约束最小方差波束形成器

考虑将MVDR中的约束条件扩展（MVDR中只有一个无畸变约束条件），来保证波束形成器更加稳健（也叫Frost Beamformer）

约束矩阵为C，维数 $N \times M_{0}$ ，第一列为无畸变约束，即 $\mathrm{g}$ 的第一个元素为 1 ，则约束条件变为:

$$\mathbf{C}^{H} \mathbf{w}=\mathbf{g}$$

目标函数依然是最小方差:

$$\min \mathbf{w}^{H} \mathbf{R}_{\mathbf{x x}}(\omega) \mathbf{w}$$

根据拉格朗日乘子法得到最优权重:

$$\mathbf{w}_{F}=\mathbf{R}_{\mathrm{XX}}^{-1}(\omega) \mathbf{C}\left(\mathbf{C}^{H} \mathbf{R}_{\mathrm{XX}}^{-1}(\omega) \mathbf{C}\right)^{-1} \mathbf{g}$$

可以看到，LCMV是一种更为通用的方案，它是对MVDR方案只有一个约束条件的特例进行了扩展。

3.4、Generalized Sidelobe Canceller (GSC)

广义旁瓣消除

LCMV的等效实现方式。从结构上将LCMV的约束优化问题转化为无约束优化问题。

方法：将LCMV的最优权重向量，分解为非自适应（固定）权重和自适应（非固定）权重两部分。非自适应权重位于约束子空间中，自适应权重位于约束子空间的正交补空间中。

约束子空间 由约束矩阵 $\mathrm{C}$ 的列向量张成， $N \times M_{0}$ ；
约束子空间的正交补空间由 $\mathbf{B} ， N \times\left(N-M_{0}\right)$ ，且满足 :

$$\begin{aligned} &\mathbf{C}^{H} \mathbf{B}=\mathbf{0} \\ &\mathbf{B}^{H} \mathbf{C}=\mathbf{0} \end{aligned}$$

我们试图将权值向量$\mathbf{w}$分解到这两个正交补空间当中。
也即，将权重向量 $\mathbf{w}$ 表示为固定分量 $\mathbf{w}_{q}$ 与自适应分量 $\mathbf{w}_{p}$ 两部分:

$$\mathbf{w}=\mathbf{w}_{q}-\mathbf{w}_{p}$$

其中， $\mathbf{w}_{q}$ 表示权重向量 $\mathbf{w}$ 向约束子空间（也就是C张成的空间）的投影:

$$\mathbf{w}_{q}=\mathbf{P}_{\mathbf{C}} \mathbf{w}=\mathbf{C}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1} \mathbf{C}^{H} \mathbf{w}=\mathbf{C}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1} \mathbf{g}$$

$\mathbf{w}_{p}$ 表示权重向量 $\mathbf{W}$ 向正交子空间（也就是B张成的空间）的投影:

$$\mathbf{w}_{p}=\mathbf{P}_{\mathbf{B}} \mathbf{w}=\mathbf{B}\left(\mathbf{B}^{H} \mathbf{B}\right)^{-1} \mathbf{B}^{H} \mathbf{w}=\mathbf{B} \mathbf{w}_{a}$$

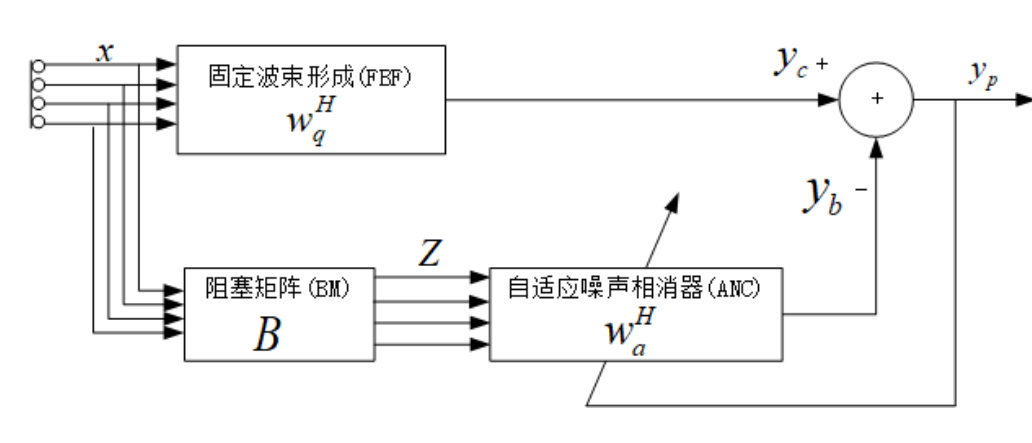
于是，我们得到GSC结构:

$$\mathbf{w}_{g s c}=\mathbf{C}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1} \mathbf{g}-\mathbf{B} \mathbf{w}_{a}=\mathbf{w}_{q}-\mathbf{B} \mathbf{w}_{a}$$

可见 GSC 得到的权值向量 由 三个要素组成

• $\mathbf{w}_{q}$ 固定波束形成分量，对应着 GSC 的固定波束形成模块。
• $\mathbf{B} $矩阵是约束空间的正交补空间，再GSC框架下，我们称之为阻塞矩阵。作用是阻塞 关键语音成分，而把干扰 露进来？
• $ \mathbf{w}_{a}$ ,是对应着GSC 自适应干扰消除模块

此外，B矩阵的选取并非唯一，

• 一种选取方式是，C矩阵已知，求取C的正交投影矩阵 ，选择正交投影矩阵的前$N-M_{0}$列

GSC 各个模块 的物理意义:

(1) FBF（固定波束形成） 用于生成 $\mathbf{w}_{q}$， 是一个 “固定旁瓣对消器”
$\mathbf{w}_{q}$，没有任何自适应成分，且满足约束条件:

$$\mathbf{C}^{H} \mathbf{w}_{q}=\mathbf{C}^{H} \mathbf{C}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1} \mathbf{g}=\mathbf{g}$$

在实际场景中，我们认为$\mathbf{w}_{q}$ 只需要有一个无畸变约束就够了，而零点约束也可以放在自适应部分，也即正交补空间的部分。当然如果我们确定干扰信号来自确定的方向时，可以扩展约束条件，追加一些零点约束，形成一些固定方向的零点，大多数时候，干扰信号方向时不知道的，所以不会这样做。

剩下两部分负责生成 与 $\mathbf{w}_{q}$，正交的部分。
即 “正交分解”，生成满足 $\mathbf{w}_{q} \perp \mathbf{B w}_{a}$条件的$\mathbf{B w}_{a}$部分，也即自适应部分 :
(2)、BM （阻塞矩阵）
(3)、ANC （自适应噪声相消器）

$$\mathbf{w}_{q}^{H} \mathbf{B} \mathbf{w}_{a}=\mathbf{g}^{H}\left(\mathbf{C}^{H} \mathbf{C}\right)^{-1} \mathbf{C}^{H} \mathbf{B} \mathbf{w}_{a}=0$$

所以：总体而言，广义旁瓣对消器(GSC) = 固定旁瓣对消器 + 与之正交的自适应旁瓣对消器

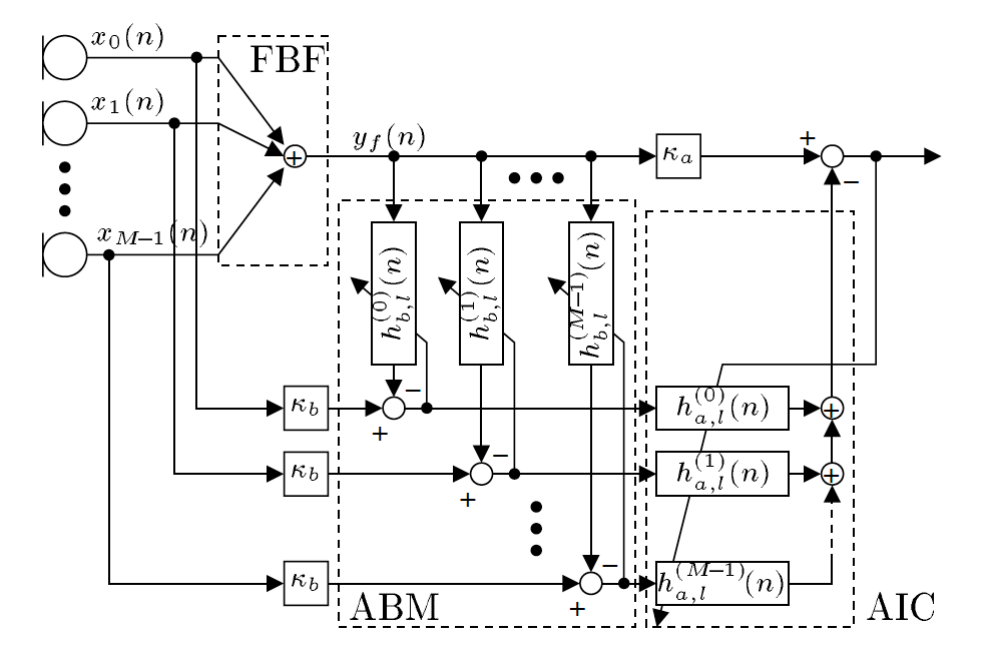
GSC的框图

由于上半部分固定，所以整个系统的关键在于阻塞矩阵$\mathbf{B}$的求解，希望通过设计阻塞矩阵使得语音信号尽可能少的泄漏到自适应部分

我们当然可以显示的求解$\mathbf{w}_{a}$的表达形式，它等价于一个无约束最优化问题：

$$\min \left(\mathbf{w}_{q}-\mathbf{B} \mathbf{w}_{a}\right)^{H} \mathbf{R}_{\mathbf{x x}}\left(\mathbf{w}_{q}-\mathbf{B} \mathbf{w}_{a}\right)$$

• GSC通过“正交分解”的方式，将LCMV约束优化问题，转化为无约束优化问题。
• “主路”和“辅路”。目标语音从“主路”通过，尽可能不要泄漏到“辅路”。
• GSC的自适应实现方式

GSC算法的实现方式：

参考：Efficient Frequency-domain realization of Robust Generalized Sidelobe Cancellers. W. Herbordt, W. Kellermann
在开源项目 Athena signal ， athena beamformer 模块 就是采用这样的方法实现的

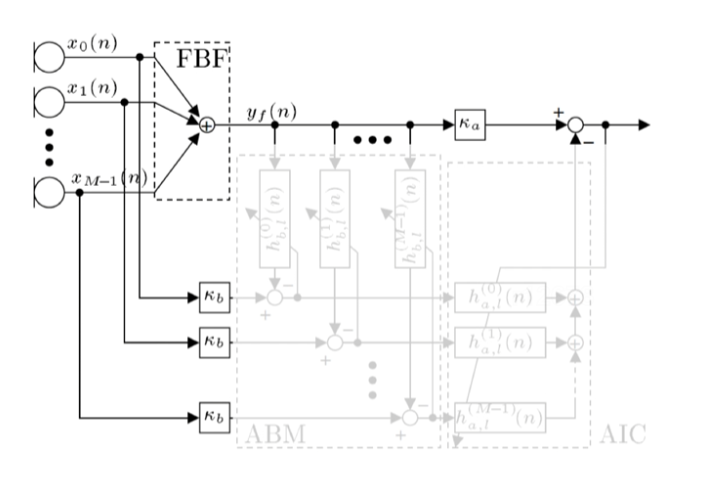
FBF- Fixed Beamforming

可以将Delay-and-sum beamformer 方案作为 固定波束形成模块

• 先决条件 ： 声源入射方向已知 （或者可以可靠的估计出来）

• 步骤：

  • 采用主波束调向（beam steering），将方向向量调整至声源入射方向，对齐每个方向的语音分量
  • 求和 得到 $y_f(n)=\sum^{M-1}_{m=0}x_m(n)$
  • 求和结果 作为 ABM模块的输入信号，以及AIC模块的期望输出信号

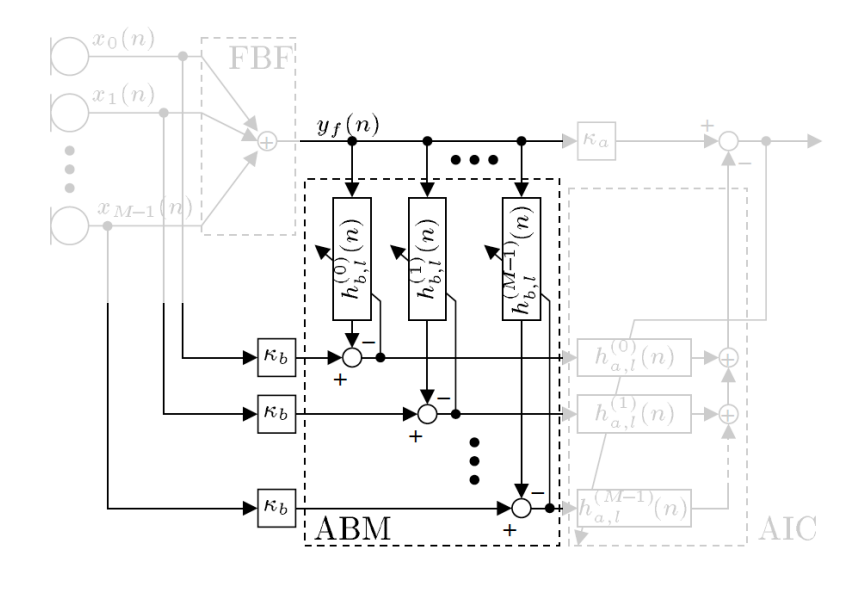
ABM – Adaptive Blocking Matrix

• 由M条通路构成
• 每条通路包含一个自适应滤波器
• 每一条通路的滤波器能够 自适应消除语音分量，而把噪声或者干扰分量尽可能保留

△ 自适应滤波输入：$y_f(n)$
△ 期望信号 ：delay of $x_m(n)$

此外，这个模块还需要一个 类似于 回声消除一样来控制自适应滤波状态的一个机制
由于目标是消除语音分量，所以只有语音存在的时候才做更新，语音不存在时仅作滤波即可。Active during speech presence

所以这就是一个典型的自适应滤波任务。我们可以利用频率自适应滤波来实现它。

以第m个通道 为例:
FBF输出 $y_{f}(n)$ 的频域表示（时域y(t)有新旧两个Block拼接而成,长度 2L）:

$$\mathbf{Y}_{f}(k)=\operatorname{diag}\left\{\mathbf{F}\left(y_{f}(k L-L), \ldots, y_{f}(k L), \ldots, y_{f}(k L+L-1)\right)^{T}\right\}$$

ABM自适应滤波器系数（由 L长 系数，后面补 L个零 拼接而成）：

$$\mathbf{H}_{b}^{(m)}(k)=\mathbf{F}\left(h_{b, 0}^{(m)}(k), \ldots, h_{b, L-1}^{(m)}(k), \quad \mathbf{0}_{1 \times L}\right)^{T},$$

滤波，频域输出信号为:

$$\mathbf{Y}_{b}^{(m)}(k)=\mathbf{Y}_{f}(k) \mathbf{H}_{b}^{(m)}(k)$$

注意到，ABM模块的输出（真正有用的）是滤波后的误差信号，下面是计算误差信号的步骤：

时域误差信号（时域上进行，期望输出减去 实际的滤波器输出）:
期望信号是第$m$个阵元的接收信号，是经过时延处理的，时延的目的是使满足时间上的因果关系。

$$\mathbf{e}_{b}^{(m)}(k)=\mathbf{x}_{m}\left(k-\frac{\kappa_{b}}{L}\right)-\mathbf{w} \mathbf{F}^{-1} \mathbf{Y}_{f}(k) \mathbf{H}_{b}^{(m)}(k)$$

其中:

$$\begin{gathered} \mathbf{w}=\operatorname{diag}\left\{\left(\mathbf{0}_{1 \times L}, \mathbf{1}_{1 \times L}\right)\right\} \\ \mathbf{x}_{m}(k)=\left(\mathbf{0}_{1 \times L}, \quad x_{m}(k L), \ldots, x_{m}(k L+L-1)\right)^{T} \end{gathered}$$

$\mathbf{w}$矩阵的目的是:只取输出的后$L$个。

则无约束ABM滤波器的更新公式:

$$\mathbf{H}_{b}^{(m)}(k+1)=\mathbf{H}_{b}^{(m)}(k)+\boldsymbol{\mu}(k) \mathbf{Y}_{f}^{H}(k) \mathbf{E}_{b}^{(m)}(k)$$

Active during speech presence

步长矩阵:

$$\boldsymbol{\mu}(k)=2 \mu \operatorname{diag}\left\{P_{0}^{-1}(k) \cdots P_{2 L-1}^{-1}(k)\right\}$$

注意这个更新过程要区分那些部分是圆周卷积，那些是线性卷积。

频点功率依旧采用迭代更新:

$$P_{l}(k)=\lambda P_{l}(k-1)+(1-\lambda)\left|Y_{f, l}(k)\right|^{2}, \quad l=0, \ldots, 2 L-1$$

$Y_{f, l}(k)$ 是 $\mathbf{Y}_{f}(k)$ 的第 $l$ 个frequency bin。

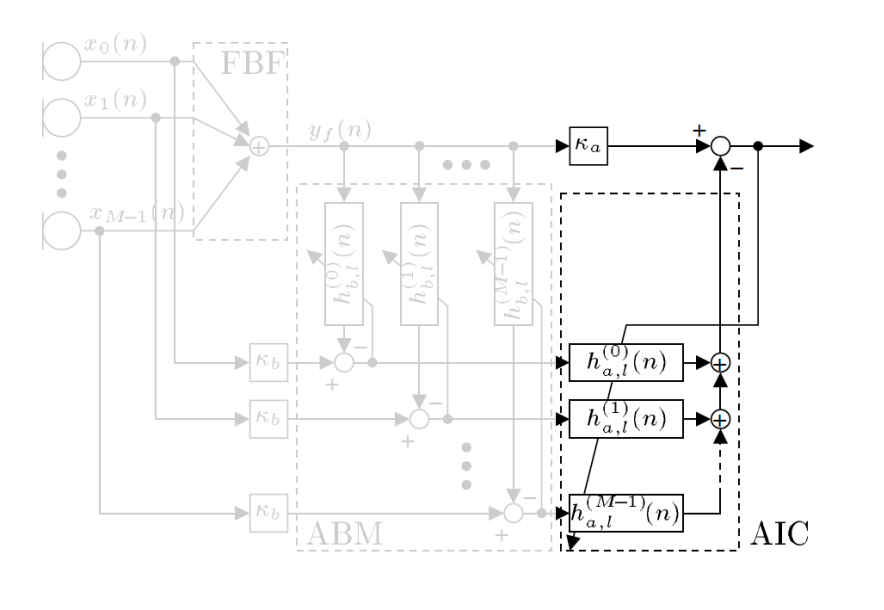
AIC – Adaptive Interference Canceller

• 由 M 条通路构成。
• 每条通路包含一个自适应滤波器：
• 自适应滤波器输出结果求和——Interference

△ 输入：ABM的输出信号 $\mathbf{E}_{b}^{(m)}(k)$ ,也即上一步 干扰信号的频域形式
△ 期望输入：delay of $y_f(n)$

这一部分是尽量提取出来接收信号中的干扰成分，所以只有干扰存在时（语音信号不存在时）才进行更新，其他时间 Active during speech absence

所以，AIC 任然可以用一种标准的 频域自适应滤波的方案来实现。

$\mathrm{AlC}$ 的输入:

$$\begin{aligned} \mathbf{X}_{a}^{(m)}(k)=\operatorname{diag}\left\{\mathbf{E}_{b}^{(m)}(k)\right.&\left.+\mathbf{J} \mathbf{E}_{b}^{(m)}(k-1)\right\}, \\ \mathbf{J}=\operatorname{diag}\left\{(1,-1,1, \ldots,-1)_{1 \times 2 L}\right\}, \end{aligned}$$

PS：可以证明，这种输入形式在时域上等价于 old block 与 new block 拼接在一起。
则AIC的时域误差信号:

$$\mathbf{e}_{a}(k)=\mathbf{y}_{f}(k)-\mathbf{y}_{a}(k),$$

其中:

$$\begin{gathered} \mathbf{y}_{f}(k)=\left(0_{1 \times L}, \quad y_{f}\left(k L-\kappa_{a}\right), \ldots, y_{f}\left(k L+L-1-\kappa_{a}\right)\right)^{T}, \\ \mathbf{y}_{a}(k)=\mathbf{W ~ F}^{-1} \sum_{m=0}^{M-1} \mathbf{X}_{a}^{(m)}(k) \mathbf{H}_{a}^{(m)}(k) \end{gathered}$$

$\mathrm{AIC}$ 自适应滤波器更新公式：

$$\mathbf{H}_{a}^{(m)}(k+1)=\mathbf{H}_{a}^{(m)}(k)+\boldsymbol{\mu}(k) \mathbf{X}_{a}^{(m) H}(k) \mathbf{E}_{a}(k),$$

步长矩阵仍然按照ABM模块的定义来做，其中频点功率按照如下方式迭代:

$$P_{l}(k)=\lambda P_{l}(k-1)+(1-\lambda) \sum_{m=0}^{M-1}\left|X_{a, l}(k)\right|^{2}$$

GSC的最终输出是AIC误差信号 $\mathbf{e}_{a}(k)$ 的后 $L$ 个点。

四、声源定位技术

所谓声源定位就是确定声源的“方位信息”

影响声源定位精度的 因素：

• 麦克风的数量
• 阵列构型以及阵列于声源的相对位置关系（如线性阵列于环形阵列对于不同角度的搜索能力有差别）
• 背景噪声和混响

从技术上看，传统的声源定位技术大致可以分为三大类（三个方向）

• Maximizing the Steered-response-power（SRP）
  最大化可控响应功率（最大化输出功率）
• High-resolution spectral-estimation
  高分辨率普估计技术
• Time difference of arrival (TDOA)
  到达时间差

摘自：Brandstein, Ward. Microphone Arrays: Signal Processing Techniques and Applications

4.1、Maximizing the Steered-response-power（SRP）

原理就是通过调向，找到一个输出功率最大的方向，认为那个方向就是声源的入射方向。
“A focused beamformer which steers the array to various locations and searches for a peak in output power.”

以 ULA主波束调向（beam steering）为例
调整频率-波数响应函数：

$$\Upsilon\left(\omega, \mathbf{k}-\mathbf{k}_{T}\right) \leftarrow \Upsilon(\omega, \mathbf{k})$$

修正权值向量:

$$\mathbf{w}_{T} \leftarrow\left[\begin{array}{c} e^{j \mathbf{k}_{T}^{T} \mathbf{p}_{0}} \\ e^{j \mathbf{k}_{T}^{T} \mathbf{p}_{1}} \\ \vdots \\ e^{j \mathbf{k}_{T}^{T} \mathbf{p}_{N-1}} \end{array}\right] \odot \mathbf{w}$$

通过空间扫描，将主波束从0°扫描至180°，只有当主瓣刚好对应到相应的声源入射方向时，输出功率才最大。

SRP-based Source Localization

方案：利用Delay-and-sum波束形成，在每一路输入信号中施加适当的延迟项，补偿声源方向到达
麦克风阵列产生的时间差，从而将各个通道中的语音信号成分时间对齐，得到输出信号。

步骤：
阵列输入信号 (共有N个阵元，下面是阵元在n时刻的采样数据):

$$\mathbf{x}(n)=\left[\begin{array}{c} x_{0}(n) \\ x_{1}(n) \\ \vdots \\ x_{N-1}(n) \end{array}\right]$$

经过Delay-and-sum波束形成后的输出信号为：

$$y(n)=\sum_{i=0}^{N-1} x_{i}\left(n+\Delta_{i}\right)$$

其中 $\Delta_{i}, i=0,1, \ldots, N-1$ 称作 steering delays（调向延时）

当我们把阵列的主波束调向至不同的空间方位时，会产生不同的调向延迟 $\Delta_{i}$ 。显然，Delay-and-sum波束形成的输出信号 $y(n)$ 与主波束的指向相关，故将其记作 $y\left(n, \mathbf{k}_{s}\right)$ ，即：

$$y\left(n, \mathbf{k}_{s}\right)=\sum_{i=0}^{N-1} x_{i}\left(n+\Delta_{i}\right)$$

实际中，由于麦克风阵列的几何布局是已知的，因此，可以选定一个麦克风作为参考麦克风，计算 声源到达各个麦克风与参考麦克风之间的到达时间差 (TDOA) ，用 $\tau$ 表示（对于ULA通常将最边上的麦克风作为参考，对于环形阵列，通常假设环形中心有一个麦克风，来作为参考），从而将计算绝对延时转 化为计算相对延时。
(7.3)式的频域等价形式为:

$$Y\left(\omega, \mathbf{k}_{s}\right)=\sum_{i=0}^{N-1} X_{i}(\omega) e^{j \omega \Delta_{i}}$$

如想将延迟求和转换为更一般的情况，卷积上一个滤波器系数即可
则频域将变成

$$Y\left(\omega, \mathbf{k}_{s}\right)=\sum_{i=0}^{N-1} G_{i}(\omega) X_{i}(\omega) e^{j \omega \Delta_{i}}$$

计算SRP :

$$P(\mathbf{k})=\int_{-\infty}^{\infty}|Y(\omega, \mathbf{k})|^{2} d \omega$$

遍历所有方向$\mathbf{k}$，Maximizing SRP :

$$\hat{\mathbf{k}}_{s}=\underset{\mathbf{k}}{\operatorname{argmax}} P(\mathbf{k})$$

“Delay-and-sum SRP” or “Filter-and-sum SRP”

以上就是SRP的基本思想以及步骤，这种方法在噪声比较弱的情况下，性能比较好。但是当噪声和混响比较大的时候性能就会恶化。

为了改进这个状况，有人利用加权的方案来优化SRP方案
借鉴GCC（广义互相关）方法中的PHAT（相位变换加权）加权思想（起到了一种白化的作用，相当于把有关幅度相关的信息全部归一化掉了，而只保留关于相位的信息，而我们所想要估计的时延其实都保留在了相位信息当中）
借鉴GCC方法中的PHAT加权思想，定义SRP-PHAT方法 :

$$P(\mathbf{k})=\sum_{i=0}^{N-1} \sum_{l=0}^{N-1} \int_{-\infty}^{\infty} \Psi_{i l}(\omega) X_{i}(\omega) X_{l}^{*}(\omega) e^{j \omega \tau_{i l}} d \omega$$

PS:这个公式相当于遍历所有可能的 阵元对（麦克风对）
其中 $\Psi_{i l}(\omega)$ 为PHAT加权函数 :

$$\Psi_{i l}(\omega)=G_{i}(\omega) G_{l}^{*}(\omega)=\frac{1}{\left|X_{i}(\omega) X_{l}^{*}(\omega)\right|}$$

上式，是SRP-PHAT的频域表达形式。相对应的时域表达形式为 :

$$P(\mathbf{k})=2 \pi \sum_{i=0}^{N-1} \sum_{l=0}^{N-1} r_{i l}\left(\tau_{i l}\right)$$

其中$ r_{i l}\left(\tau_{i l}\right)$是 广义互相关函数
后面的步骤和标准的 SRP一样了，都是遍历所有方向然后 找最大的方向。

SRP-PHAT相当于 N 元麦克风阵列中，对于入射方位𝐤而言，计算所有可能的“麦克风对”（possible pairwise）的广义互相关函数之和（还包括N个零延时的广义自相关函数之和）。
对于只有两个麦克风所组成的阵列，SRP-PHAT等价于广义互相关法（GCC）。随着麦克风数目的增多，GCC方法扩展成为SRP-PHAT方法。
SRP-PHAT运算量偏大，通常需要权衡搜索精度和运算量之间的关系

4.2、High-resolution spectral estimation

即基于高分辨率普估计的声源定位技术。
这种技术分为两个大的子方向。

• 1、Minimum variance (MV) spectral estimation （基于最小方差的谱估计技术）
• 2、Eigen-analysis-based techniques （基于特征值分析的谱估计是几乎）

无论哪种方向，计算的核心都是对于阵列信号相关矩阵$\mathbf{R}_{\mathbf{xx}}$的估计。

功率谱密度描述信号功率随频率的分布，是信号的一种频域表示。由于阵列信号处理的主要任务之一是信号的空间参数估计（如DOA估计），所以将功率谱密度的概念在空域加以延伸就显得十分重要。这种广义的功率谱常简称为空间谱。空间谱描述了信号的空间参数的分布。

回顾MVDR Beamformer：

$$\mathbf{w}_{c}=\frac{\mathbf{R}_{\mathbf{X X}}^{-1}(\omega) \mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{s}\right)}{\mathbf{v}_{\mathbf{k}}^{H}\left(\mathbf{k}_{s}\right) \mathbf{R}_{\mathbf{X X}}^{-1}(\omega) \mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{s}\right)}$$

MVDR使得目标方向以外的任何干扰贡献的功率最小，同时保持目标方向上的信号功率（无畸变约束，保持目标方向上的功率不变），可视为一种空间带通滤波器。
MVDR最优波束形成的必要条件 : 波达方向 $\mathbf{k}_{s}$ 的估计。

最优权重 $\mathbf{w}_{c}$ ，带入输出功率当中，得到以下的阵列输出功率 :

$$P\left(\mathbf{k}_{s}\right)=\mathbf{w}_{c}^{H} \mathbf{R}_{\mathbf{x x}}(\omega) \mathbf{w}_{c}=\frac{1}{\mathbf{v}_{\mathbf{k}}^{H}\left(\mathbf{k}_{s}\right) \mathbf{R}_{\mathbf{x x}}^{-1}(\omega) \mathbf{v}_{\mathbf{k}}\left(\mathbf{k}_{s}\right)}$$

可以把上式视为一种“空间功率谱”，以空间方位$\mathbf{k}_{s}$的变化而变化。
定义这种功率谱为 “空间功率谱”（Capon 谱）

$$P_{\text {Capon }}(\mathbf{k})=\frac{1}{\mathbf{v}_{\mathbf{k}}^{H}(\mathbf{k}) \mathbf{R}_{\mathbf{x X}}^{-1}(\omega) \mathbf{v}_{\mathbf{k}}(\mathbf{k})}$$

其峰值对应的入射方向就是声源的入射方向：

$$\hat{\mathbf{k}}_{S}=\underset{\mathbf{k}}{\operatorname{argmax}} P_{\text {Capon }}(\mathbf{k})$$

这就是基于最小方差（MV ) 的空间谱估计方法。

在这个方向中衍生出一种 基于特征值分析的方法 : multiple signal classification，MUSIC 算法

$$P_{\text {MUSIC }}(\mathbf{k})=\frac{1}{\mathbf{v}_{\mathbf{k}}^{H}(\mathbf{k}) \mathbf{G G}^{H} \mathbf{v}_{\mathbf{k}}(\mathbf{k})}$$

其中$\mathbf{G}$是我们算出自相关矩阵之后，通过特征值 求取的噪声子空间。

TDOA-based Source Localization

基于到达时间差的声源定位

到达时间差（time difference of arrival,DOA）
时延估计（time dealy estimation，TDE）

原理

仅根据时延$\tau$就可以倒推出方向$\theta$

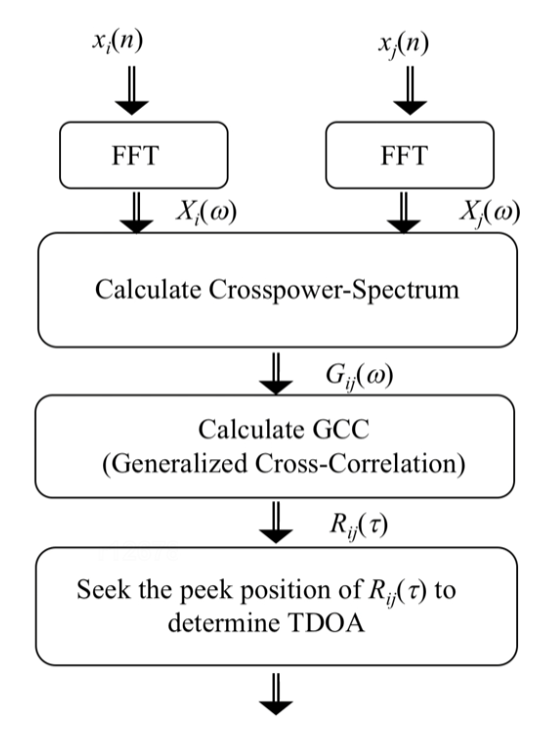
再次回顾GCC(Generalized cross correlation)方案估计时延差

$$R_{i j}(\tau)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \Psi_{i j}(\omega) X_{i}(\omega) X_{j}^{*}(\omega) e^{j \omega \tau} d \omega$$